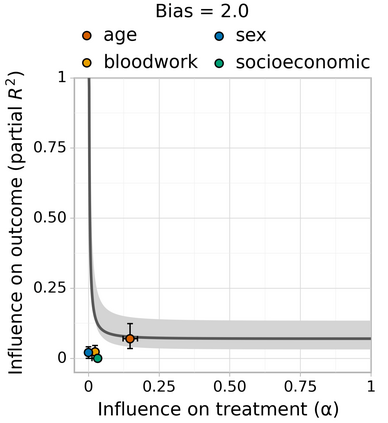
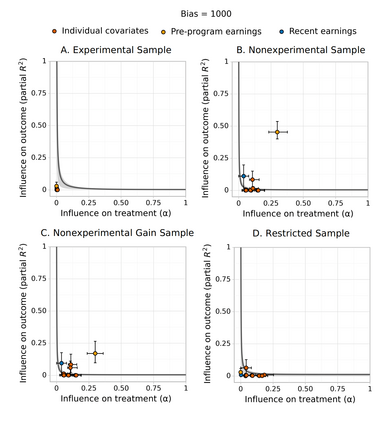
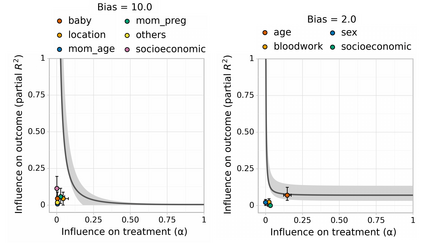
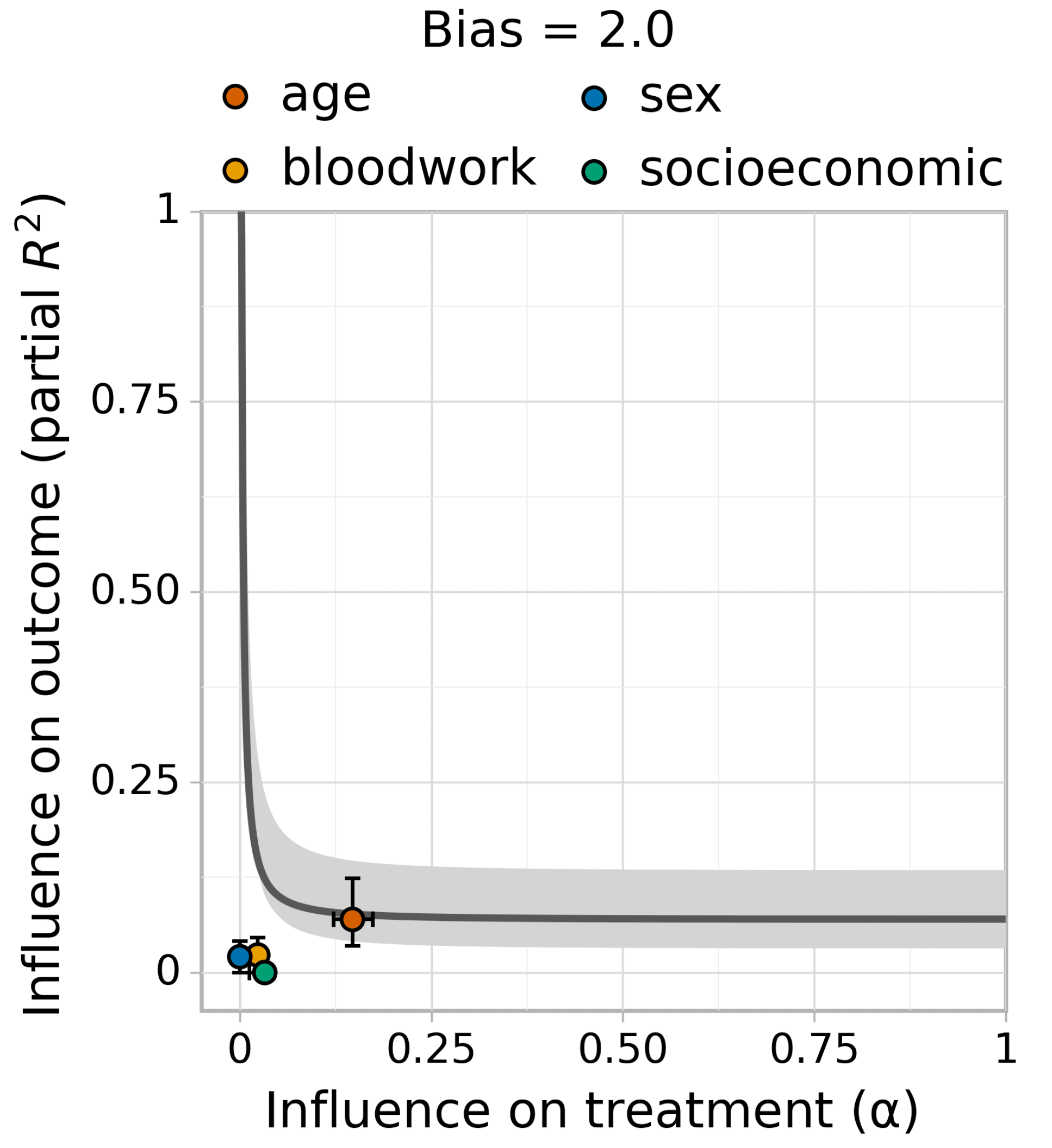
It is a truth universally acknowledged that an observed association without known mechanism must be in want of a causal estimate. However, causal estimation from observational data often relies on the (untestable) assumption of `no unobserved confounding'. Violations of this assumption can induce bias in effect estimates. In principle, such bias could invalidate or reverse the conclusions of a study. However, in some cases, we might hope that the influence of unobserved confounders is weak relative to a `large' estimated effect, so the qualitative conclusions are robust to bias from unobserved confounding. The purpose of this paper is to develop \emph{Austen plots}, a sensitivity analysis tool to aid such judgments by making it easier to reason about potential bias induced by unobserved confounding. We formalize confounding strength in terms of how strongly the confounder influences treatment assignment and outcome. For a target level of bias, an Austen plot shows the minimum values of treatment and outcome influence required to induce that level of bias. Domain experts can then make subjective judgments about whether such strong confounders are plausible. To aid this judgment, the Austen plot additionally displays the estimated influence strength of (groups of) the observed covariates. Austen plots generalize the classic sensitivity analysis approach of Imbens [Imb03]. Critically, Austen plots allow any approach for modeling the observed data and producing the initial estimate. We illustrate the tool by assessing biases for several real causal inference problems, using a variety of machine learning approaches for the initial data analysis. Code is available at https://github.com/anishazaveri/austen_plots
翻译:众所周知,一个没有已知机制的观察协会必须缺乏因果估计,但观察数据的因果估计往往依赖于“不可检验的”“不可观察到的因果关系估计”的假设,违反这一假设可能会引起效果估计的偏差。原则上,这种偏差可能使一项研究的结论失效或逆转。然而,在某些情况下,我们可能希望,未观察到的混淆者的影响相对于“大”估计效果而言是微弱的,因此质量结论是强烈的,从未观察到的混结中产生偏差。本文的目的是发展(不可检验的)“不可测的)“不可测的”的“不可测的”估计的“因果关系图案 ”, 这是一种敏感分析工具, 帮助做出这种判断, 使人们更容易理解由未观测到的“网状”引发的潜在偏差。 对于目标的偏差程度, Austen 地图显示治疗和结果影响所需的最起码的模型值,从而导致这种偏差程度。 由专家就这种强烈的初始折算术是否可信作出主观判断。