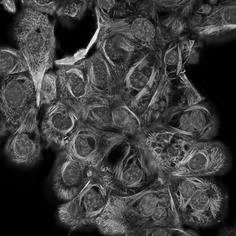
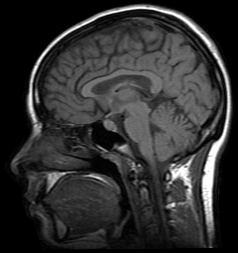
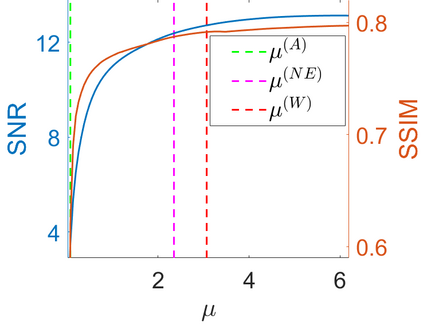
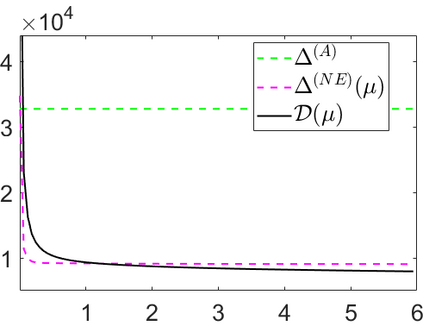
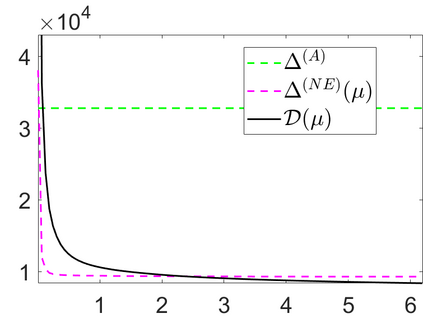
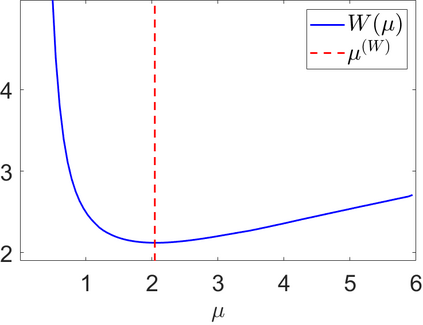
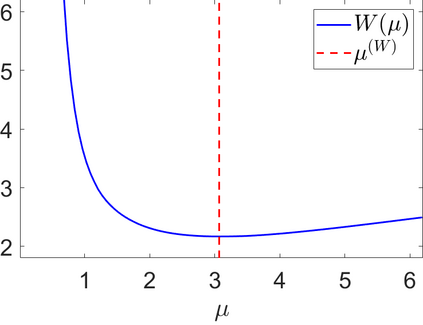
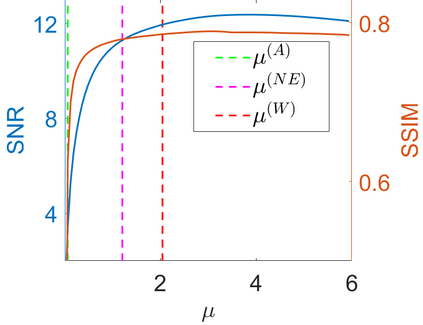
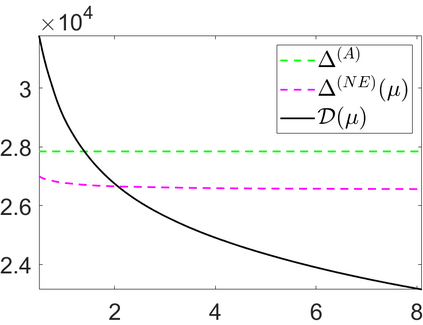
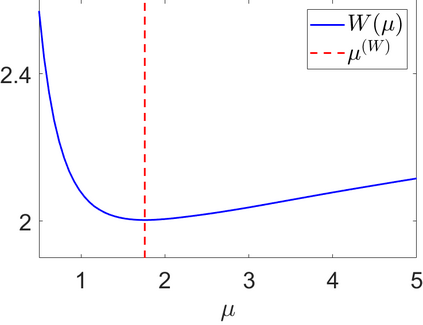
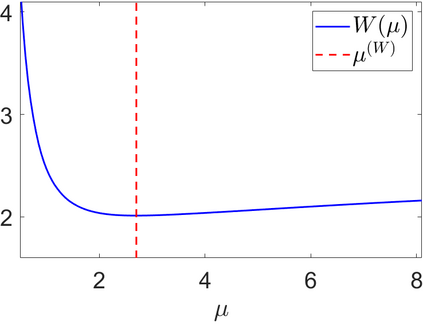
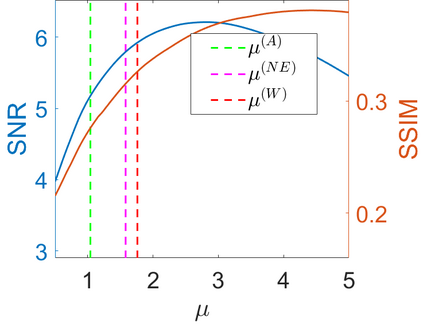
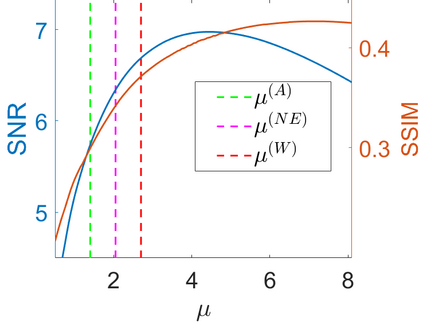
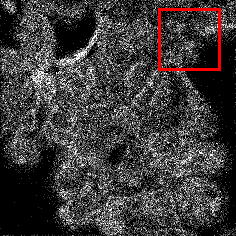
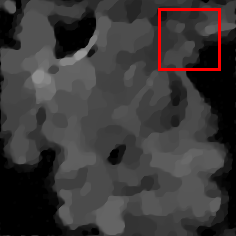
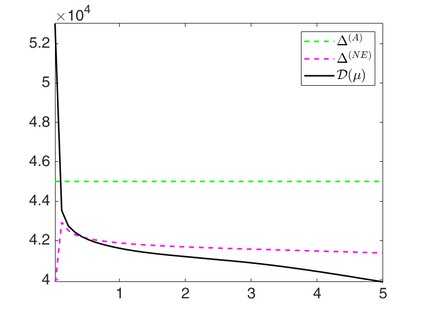
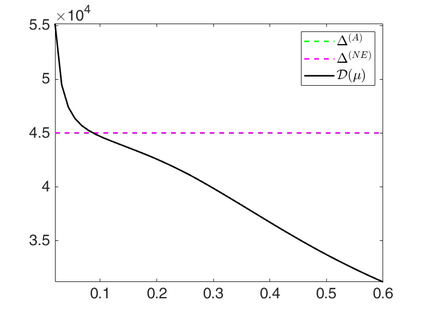
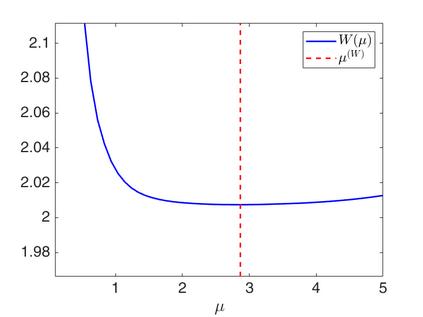
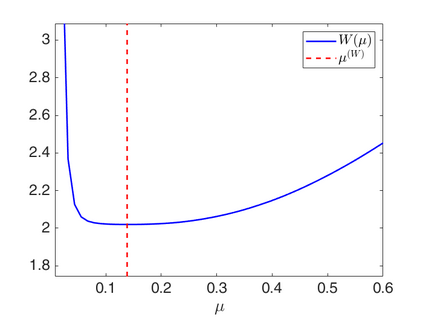
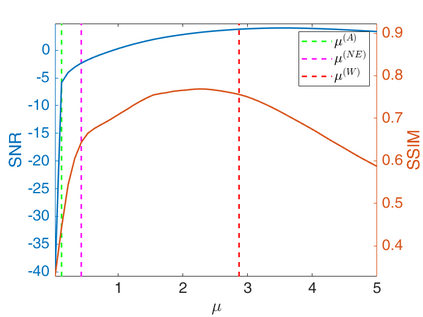
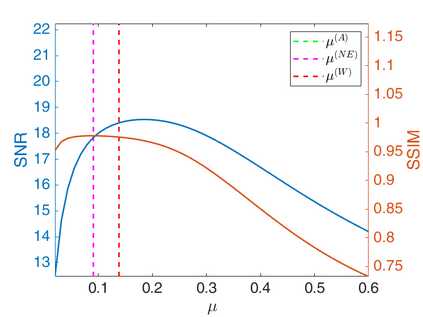
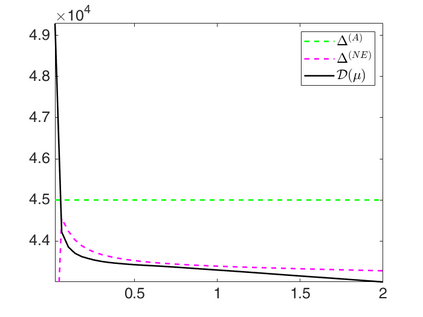
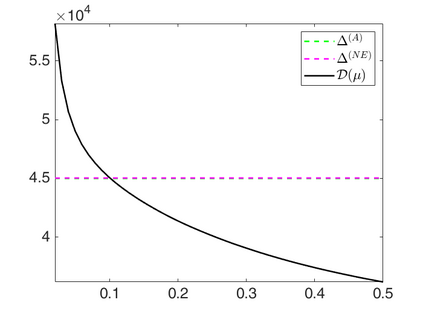
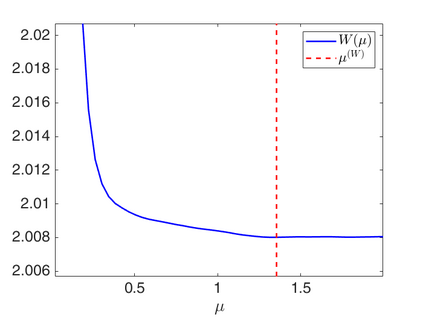
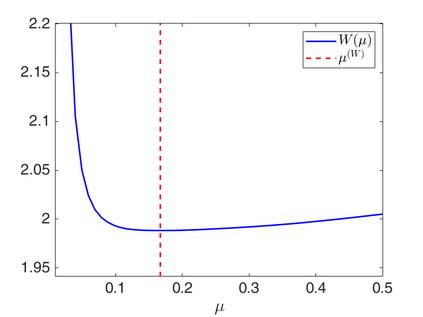
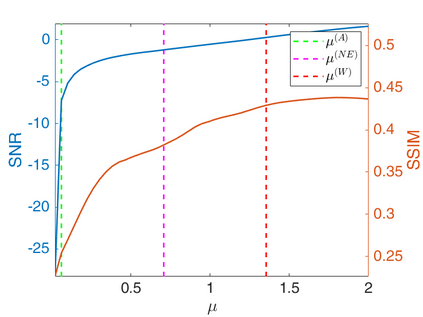
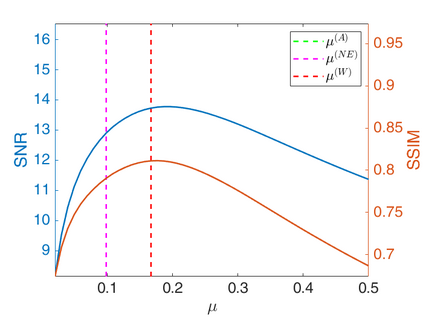
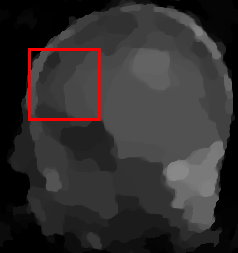
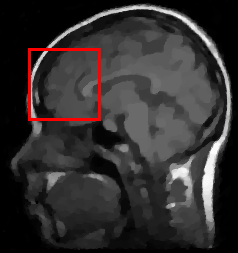
We propose a novel automatic parameter selection strategy for variational imaging problems under Poisson noise corruption. The selection of a suitable regularization parameter, whose value is crucial in order to achieve high quality reconstructions, is known to be a particularly hard task in low photon-count regimes. In this work, we extend the so-called residual whiteness principle originally designed for additive white noise to Poisson data. The proposed strategy relies on the study of the whiteness property of a standardized Poisson noise process. After deriving the theoretical properties that motivate our proposal, we solve the target minimization problem with a linearized version of the alternating direction method of multipliers, which is particularly suitable in presence of a general linear forward operator. Our strategy is extensively tested on image restoration and computed tomography reconstruction problems, and compared to the well-known discrepancy principle for Poisson noise proposed by Zanella at al. and with a nearly exact version of it previously proposed by the authors.
翻译:我们为Poisson噪音腐败下的变异成像问题提出了一个新的自动参数选择战略。选择一个适当的正规化参数(其价值对于实现高质量的重建至关重要)被认为是低光子计数制度下的一项特别艰巨的任务。在这项工作中,我们把最初为添加白噪音而设计的所谓残余白化原则扩大到Poisson数据。拟议战略依赖于对标准化Poisson噪音过程的白质特性的研究。在得出激励我们提案的理论属性之后,我们用一种直线化的乘数交替方向方法来解决目标最小化问题,这种方法在一般线性前方操作者面前特别合适。我们的战略在图像恢复和计算图象重建问题上进行了广泛的测试,并与Zanella al提出的众所周知的Poisson噪音差异原则以及作者先前提出的几乎准确版本。