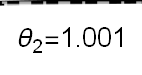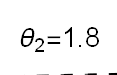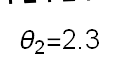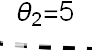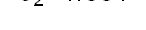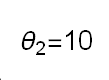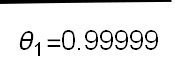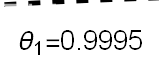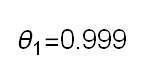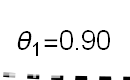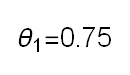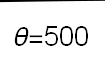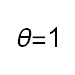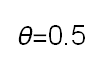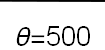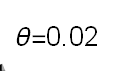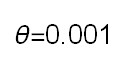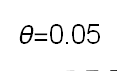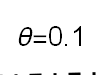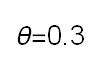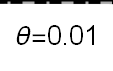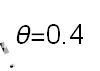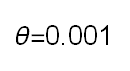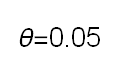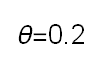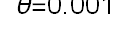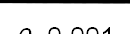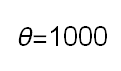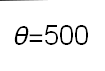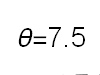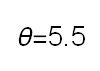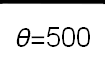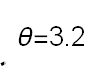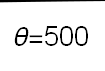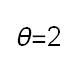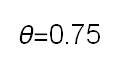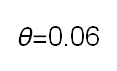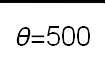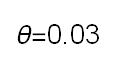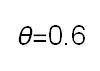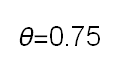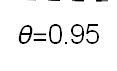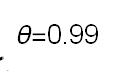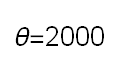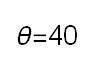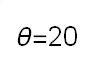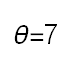Asymmetric Laplace scale mixtures for the distribution of cryptocurrency returns

Recent studies about cryptocurrency returns show that its distribution can be highly-peaked, skewed, and heavy-tailed, with a large excess kurtosis. To accommodate all these peculiarities, we propose the asymmetric Laplace scale mixture (ALSM) family of distributions. Each member of the family is obtained by dividing the scale parameter of the conditional asymmetric Laplace (AL) distribution by a convenient mixing random variable taking values on all or part of the positive real line and whose distribution depends on a parameter vector $\boldsymbol{\theta}$ providing greater flexibility to the resulting ALSM. Advantageously with respect to the AL distribution, the members of our family allow for a wider range of values for skewness and kurtosis. For illustrative purposes, we consider different mixing distributions; they give rise to ALSMs having a closed-form probability density function where the AL distribution is obtained as a special case under a convenient choice of $\boldsymbol{\theta}$. We examine some properties of our ALSMs such as hierarchical and stochastic representations and moments of practical interest. We describe an EM algorithm to obtain maximum likelihood estimates of the parameters for all the considered ALSMs. We fit these models to the returns of two cryptocurrencies, considering several classical distributions for comparison. The analysis shows how our models represent a valid alternative to the considered competitors in terms of AIC, BIC, and likelihood-ratio tests.