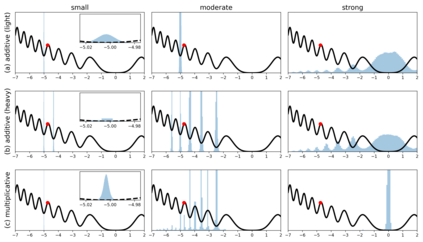
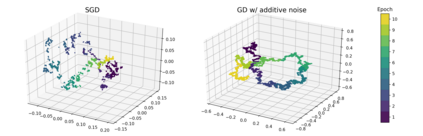
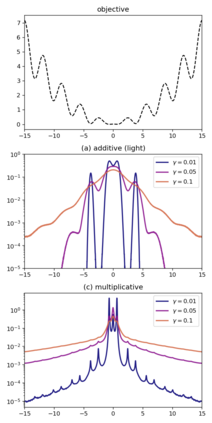
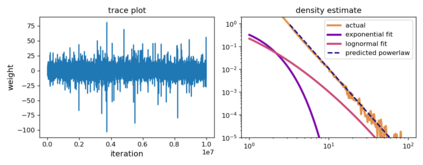
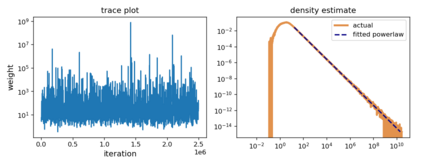
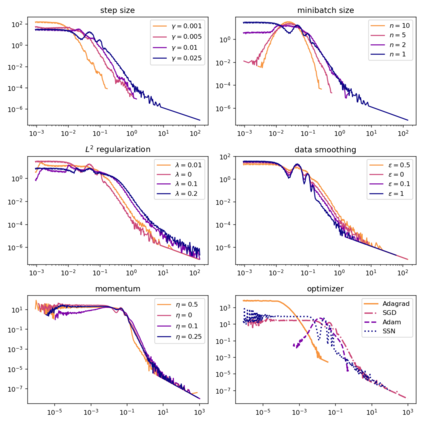
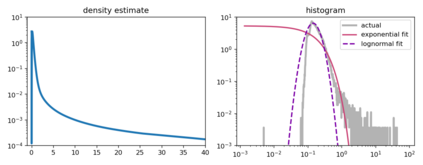
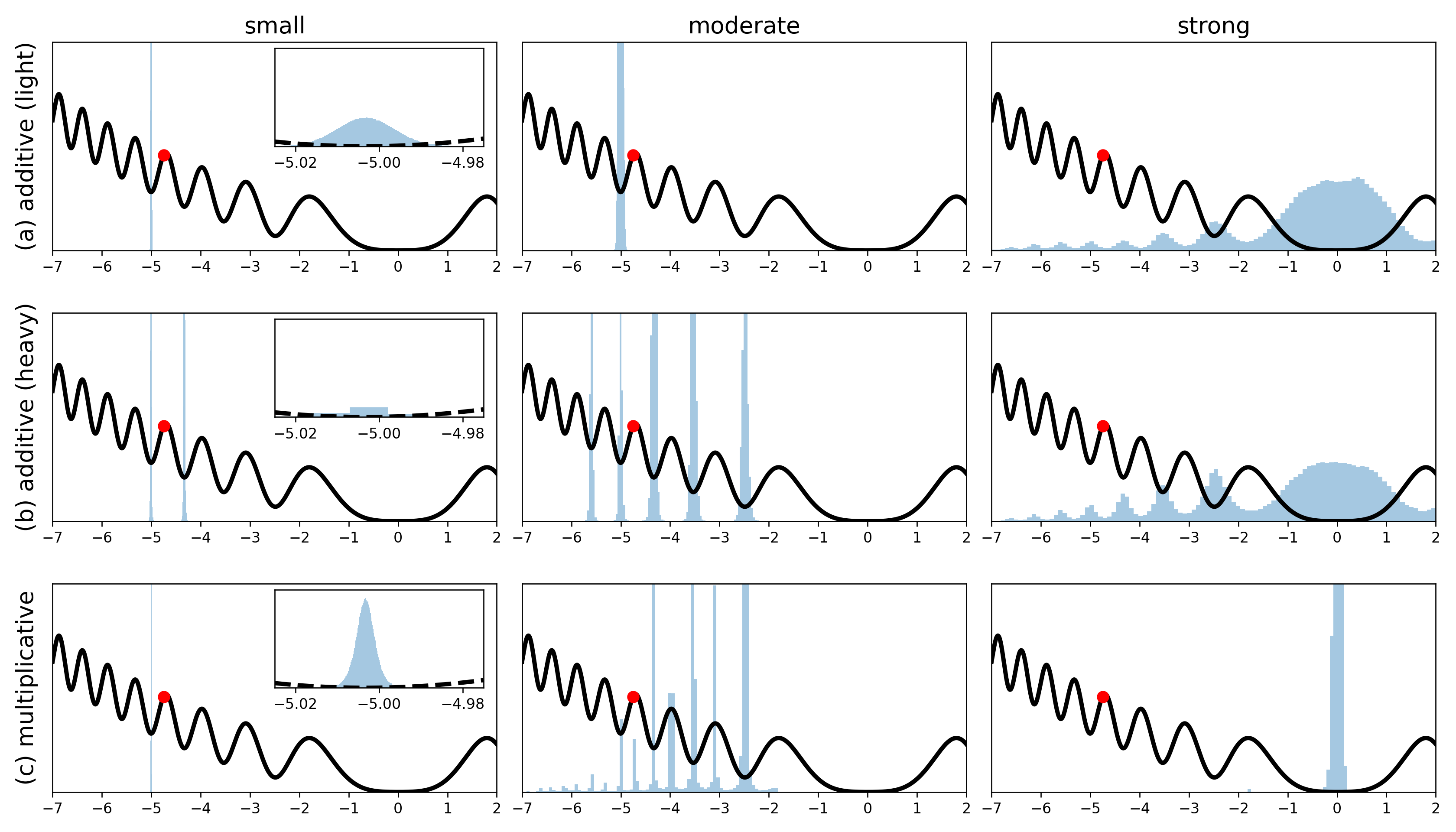
Although stochastic optimization is central to modern machine learning, the precise mechanisms underlying its success, and in particular, the precise role of the stochasticity, still remain unclear. Modelling stochastic optimization algorithms as discrete random recurrence relations, we show that multiplicative noise, as it commonly arises due to variance in local rates of convergence, results in heavy-tailed stationary behaviour in the parameters. A detailed analysis is conducted for SGD applied to a simple linear regression problem, followed by theoretical results for a much larger class of models (including non-linear and non-convex) and optimizers (including momentum, Adam, and stochastic Newton), demonstrating that our qualitative results hold much more generally. In each case, we describe dependence on key factors, including step size, batch size, and data variability, all of which exhibit similar qualitative behavior to recent empirical results on state-of-the-art neural network models from computer vision and natural language processing. Furthermore, we empirically demonstrate how multiplicative noise and heavy-tailed structure improve capacity for basin hopping and exploration of non-convex loss surfaces, over commonly-considered stochastic dynamics with only additive noise and light-tailed structure.
翻译:尽管随机优化是现代机器学习的核心,但其成功背后的确切机制,特别是其准确的随机性的作用仍然不清楚。 模拟随机随机重复关系中的模拟随机优化算法,我们表明,由于当地趋同率的差异,通常会产生多倍噪音,因此在参数中造成重尾固定行为。对应用到简单线性回归问题的SGD进行了详细分析,随后对更大规模的模型(包括非线性和非线性和非线性)和优化器(包括动力、亚当和牛顿)和优化器(包括动力、亚当和软性牛顿)进行了理论分析,表明我们的质量效果大得多。在每种情况下,我们描述对关键因素的依赖性,包括步数大小、批量大小和数据变异性,所有这些都显示出与计算机视觉和自然语言处理中的最新神经网络模型的经验性分析结果相似的质量行为。此外,我们从经验上证明,多倍增噪声和重成型结构如何提高盆地选择和探索非convex损失地平面结构的能力,只有超常考虑的硬度和超常的硬度结构。