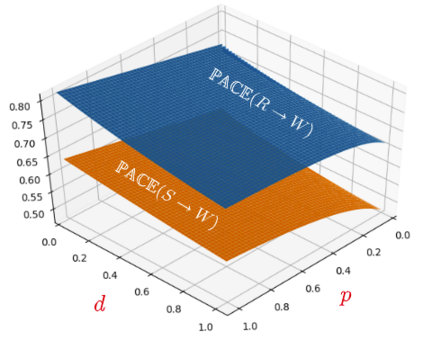
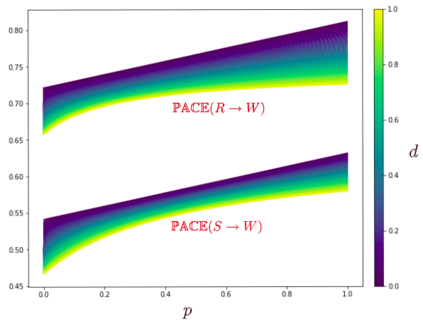
In this paper, we introduce a new causal framework capable of dealing with probabilistic and non-probabilistic problems. Indeed, we provide a formula called Probabilistic vAriational Causal Effect (PACE). Our formula of causal effect uses the idea of total variation of a function integrated with probability theory. PACE has a parameter $d$ determining the degree of being probabilistic. The lower values of $d$ refer to the scenarios that rare cases are important. In contrast, with the higher values of $d$, our model deals with the problems that are in nature probabilistic. Hence, instead of a single value for causal effect, we provide a causal effect vector by discretizing $d$. We also address the problem of computing counterfactuals in causal reasoning. We compare our model to the Pearl model, the mutual information model, the conditional mutual information model, and the Janzing et al. model by investigating several examples.
翻译:在本文中,我们引入了一个新的因果框架,能够处理概率和非概率问题。事实上,我们提供了一种叫做概率与因果关系效应(PACE)的公式。我们的因果效应公式使用了与概率理论结合的函数整体变化的概念。PACE有一个参数,以美元确定概率的程度。美元这一较低值是指罕见案例的假设情况。相反,由于美元值较高,我们的模型处理的是自然概率问题。因此,我们通过分离美元而不是单一值来提供因果关系矢量。我们还解决了在因果推理中计算反事实的问题。我们将我们的模型与珍珠模型、相互信息模型、有条件的相互信息模型和Janzing等人模型相比较,我们通过调查几个例子。