A Full Characterization of Excess Risk via Empirical Risk Landscape

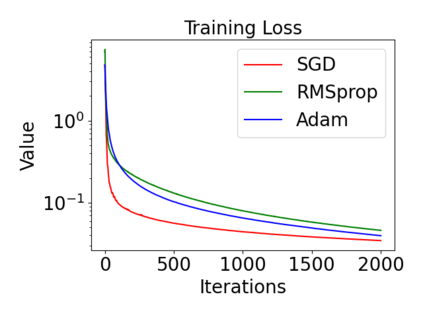
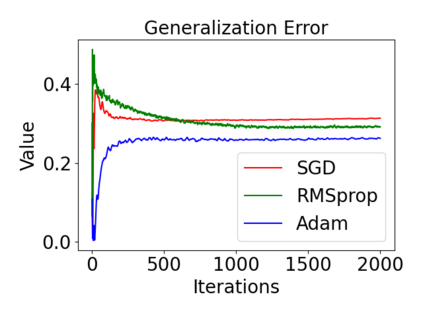
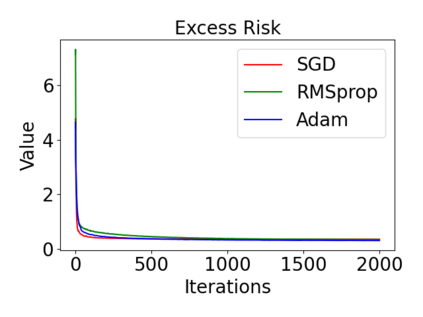
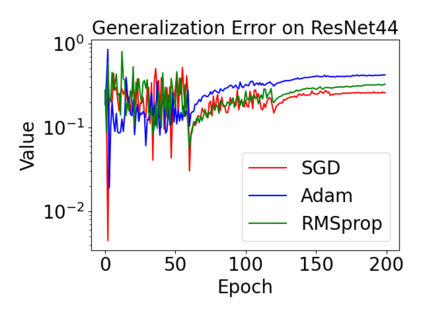
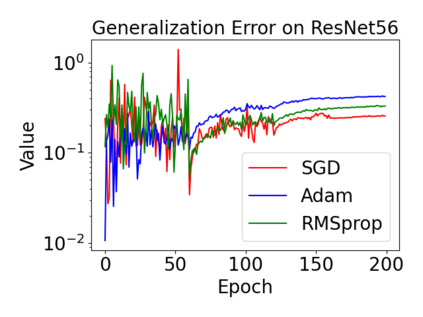
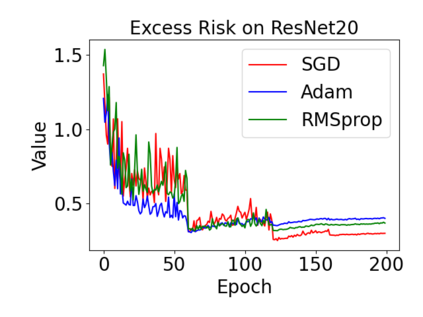
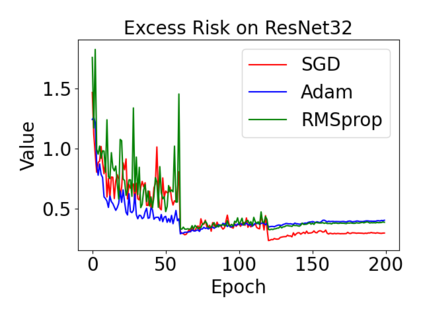
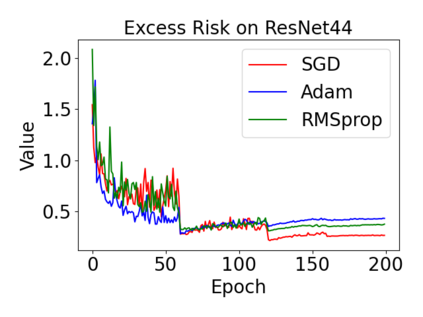
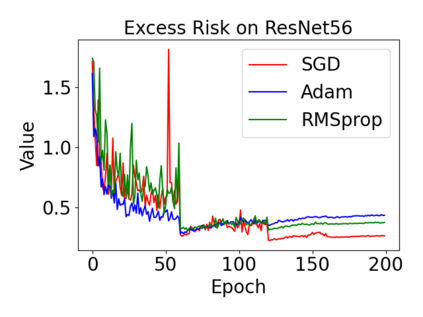
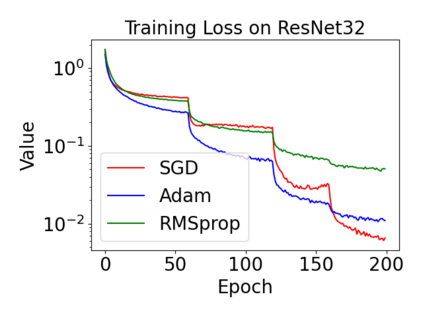
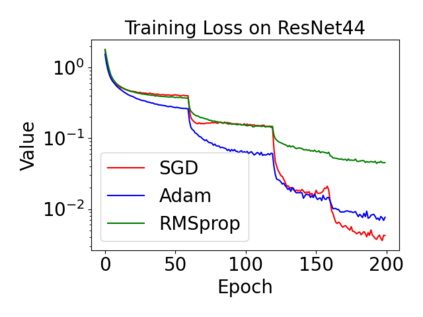
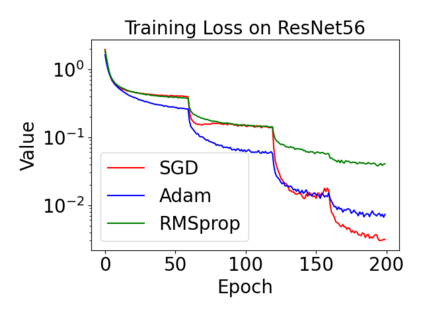
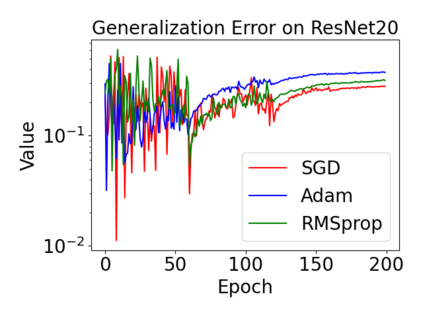
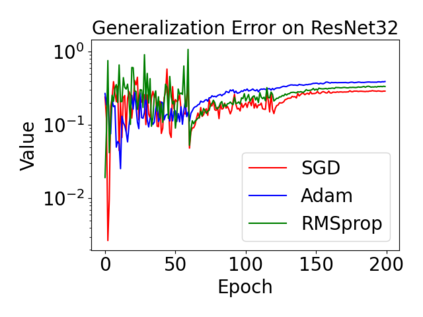
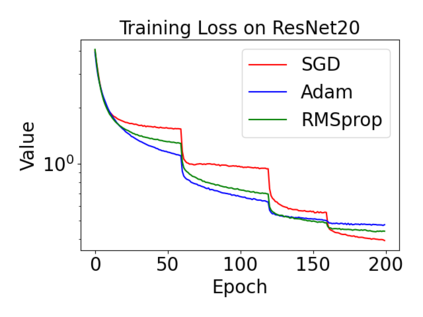
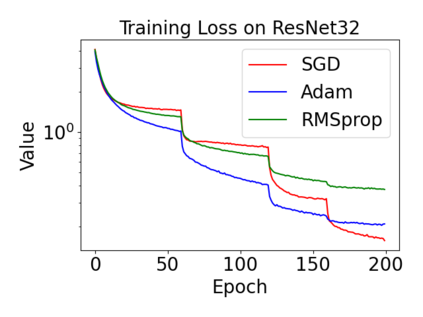
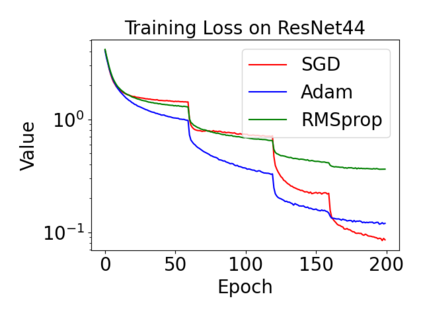
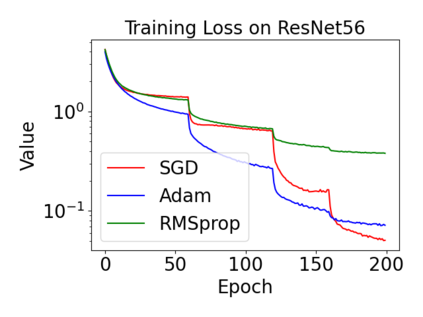
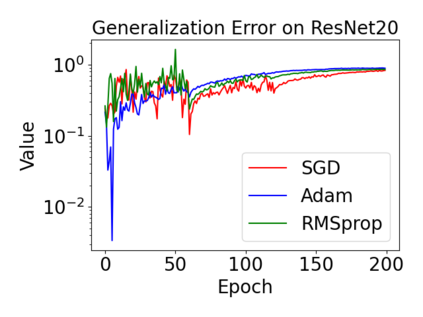
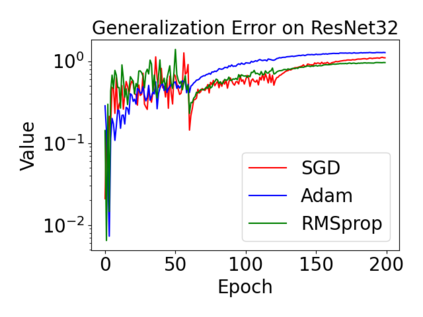
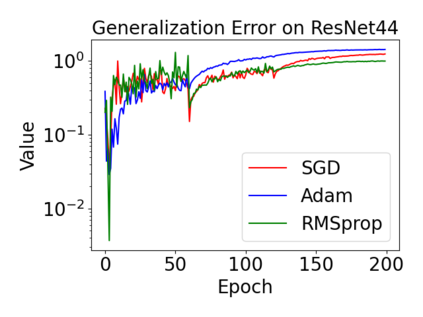
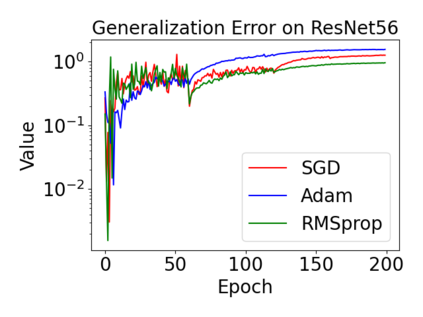
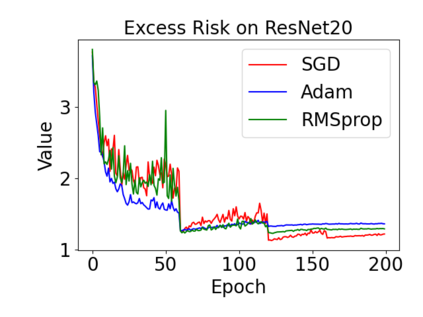
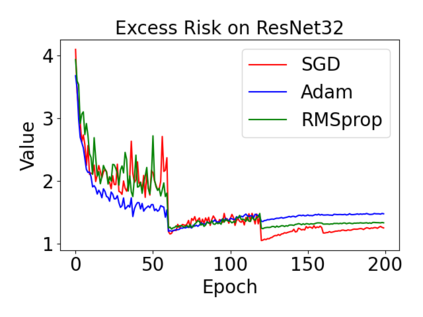
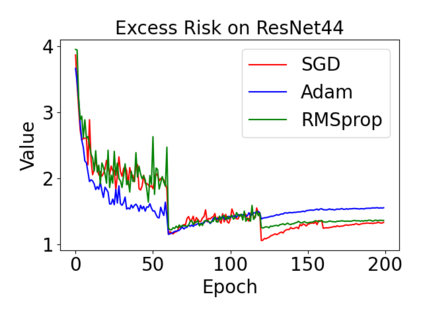
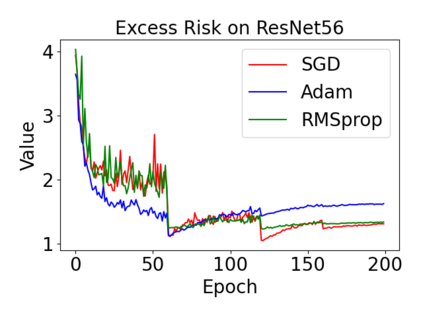
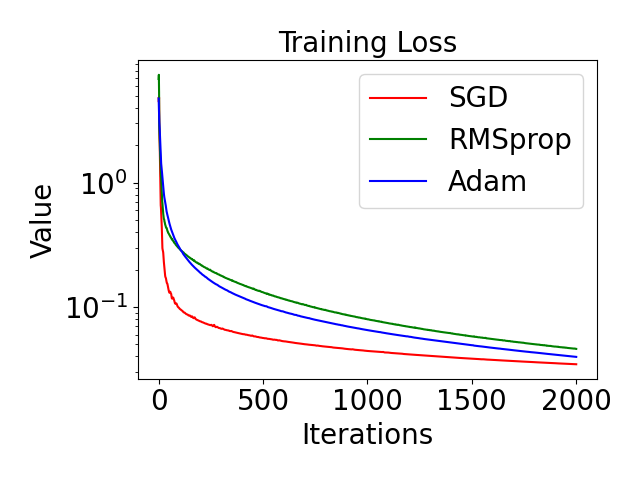
In this paper, we provide a unified analysis of the excess risk of the model trained by a proper algorithm with both smooth convex and non-convex loss functions. In contrast to the existing bounds in the literature that depends on iteration steps, our bounds to the excess risk do not diverge with the number of iterations. This underscores that, at least for smooth loss functions, the excess risk can be guaranteed after training. To get the bounds to excess risk, we develop a technique based on algorithmic stability and non-asymptotic characterization of the empirical risk landscape. The model obtained by a proper algorithm is proved to generalize with this technique. Specifically, for non-convex loss, the conclusion is obtained via the technique and analyzing the stability of a constructed auxiliary algorithm. Combining this with some properties of the empirical risk landscape, we derive converged upper bounds to the excess risk in both convex and non-convex regime with the help of some classical optimization results.