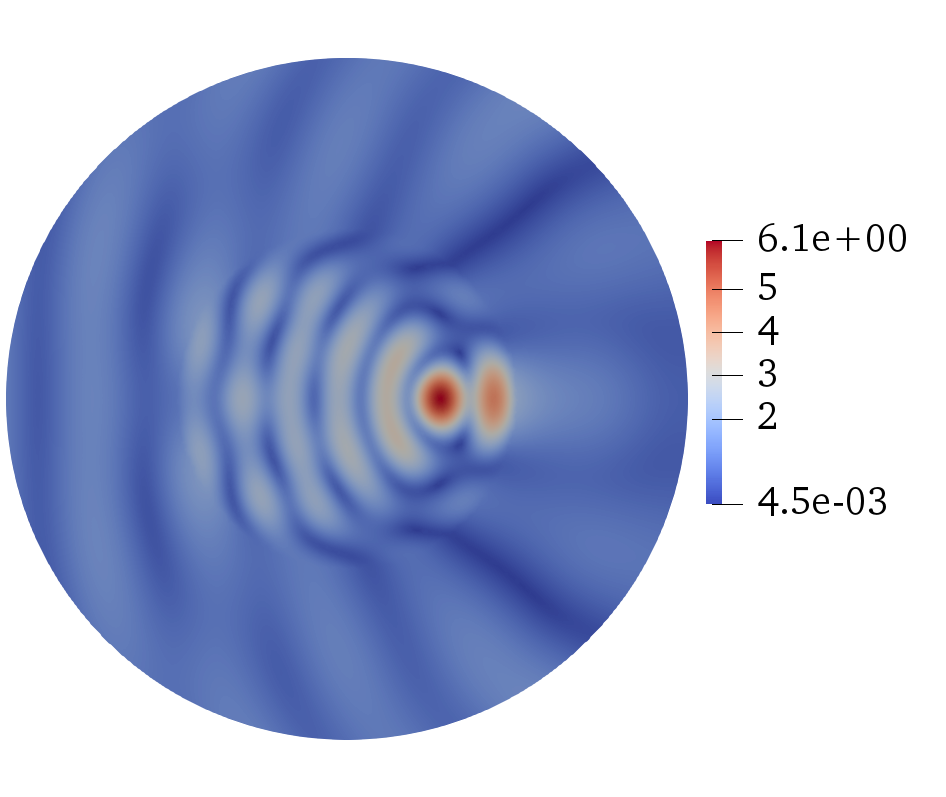
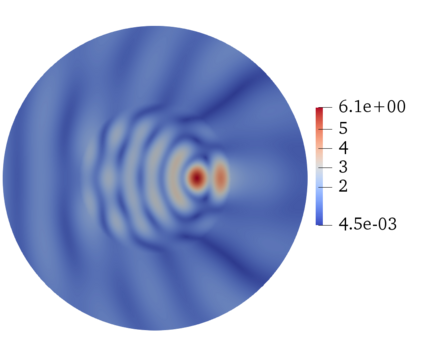
In the field of Domain Decomposition (DD), Optimized Schwarz Method (OSM) appears to be one of the prominent techniques to solve large scale time-harmonic wave propagation problems. It is based on appropriate transmission conditions using carefully designed impedance operators to exchange information between sub-domains. The efficiency of such methods is however hindered by the presence of cross-points, where more than two sub-domains abut, if no appropriate treatment is provided. In this work, we propose a new treatment of the cross-point issue for the Helmholtz equation that remains valid in any geometrical interface configuration. We exploit the multi-trace formalism to define a new exchange operator with suitable continuity and isometry properties. We then develop a complete theoretical framework that generalizes classical OSM to partitions with cross points and contains a rigorous proof of geometric convergence, uniform with respect to the mesh discretization, for appropriate positive impedance operators. Extensive numerical results in 2D and 3D are provided as an illustration of the performance of the proposed method.
翻译:在DD领域,优化施瓦兹法似乎是解决大规模时温波传播问题的突出技术之一,其基础是适当的传输条件,使用精心设计的阻力操作器,在分界之间交流信息;然而,由于存在交叉点,这些方法的效率受到阻碍,在未提供适当处理的情况下,有超过两个分界,但同时又有超过两个分界的分界点;在这项工作中,我们提议对Helmholtz方程式的交叉点问题采取新的处理办法,该办法在任何几何界面配置中仍然有效;我们利用多轨形式主义来确定一个新的交换操作器,具有适当的连续性和异度特性;然后我们开发一个完整的理论框架,将典型的OSM与交叉点隔开,并载有严格的几何趋同证据,与网格分解一致,以适当积极的阻力操作器一致;提供了2D和3D的广泛数字结果,以说明拟议方法的性能。