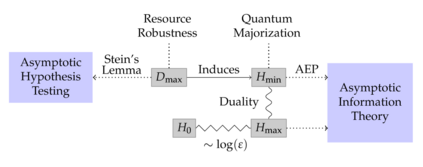
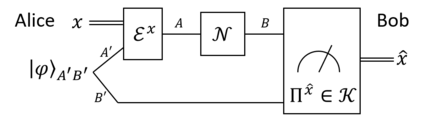
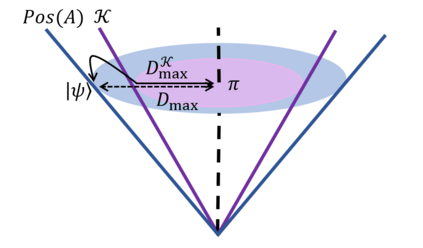
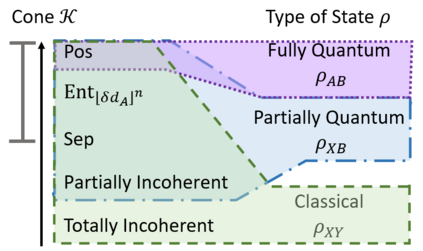
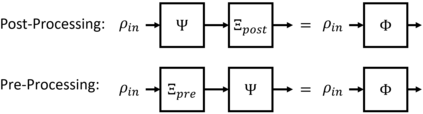
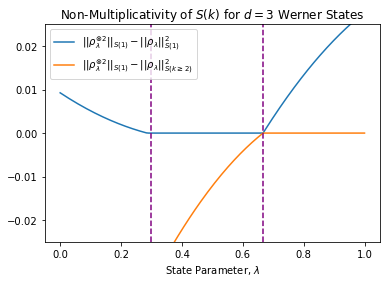
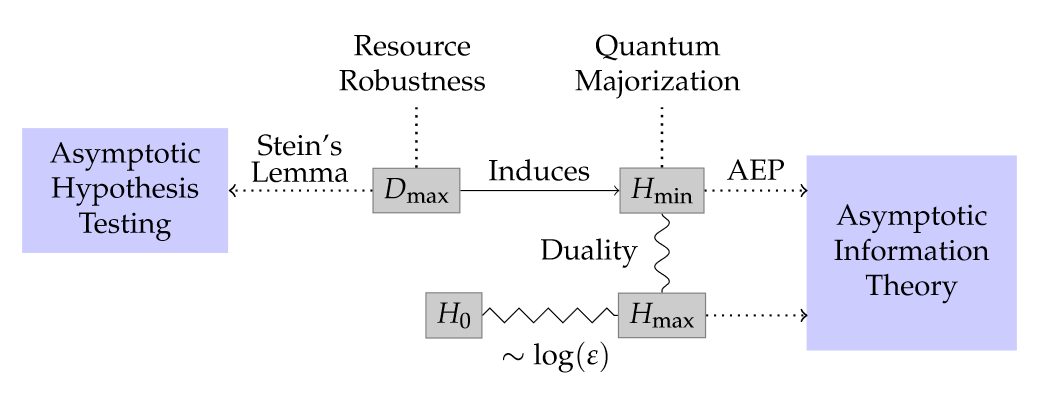
The max-relative entropy and the conditional min-entropy it induces have become central to one-shot information theory. Both may be expressed in terms of a conic program over the positive semidefinite cone. Recently, it was shown that the same conic program altered to be over the separable cone admits an operational interpretation in terms of communicating classical information over a quantum channel. In this work, we generalize this framework of replacing the cone to determine which results in quantum information theory rely upon the positive semidefinite cone and which can be generalized. We show the fully quantum Stein's lemma and asymptotic equipartition property break down if the cone exponentially increases in resourcefulness but never approximates the positive semidefinite cone. However, we show for CQ states, the separable cone is sufficient to recover the asymptotic theory, thereby drawing a strong distinction between the fully and partial quantum settings. We present parallel results for the extended conditional min-entropy. In doing so, we extend the notion of k-superpositive channels to superchannels. We also present operational uses of this framework. We first show the cone restricted min-entropy of a Choi operator captures a measure of entanglement-assisted noiseless classical communication using restricted measurements. We show that quantum majorization results naturally generalize to other cones. As a novel example, we introduce a new min-entropy-like quantity that captures the quantum majorization of quantum channels in terms of bistochastic pre-processing. Lastly, we relate this framework to general conic norms and their non-additivity. Throughout this work we emphasize the introduced measures' relationship to general convex resource theories. In particular, we look at both resource theories that capture locality and resource theories of coherence/Abelian symmetries.
翻译:最大阻燃剂和它诱发的有条件微粒质素已经成为一发信息理论的核心。 两者都可能表现为正半无极锥体的二次曲线模型。 最近, 显示同样的二次曲线模型被改变为分解锥体的同一二次曲线模型在通过量子频道传播古典信息方面承认了一种实用的解释。 在这项工作中, 我们推广了替换锥体的框架, 以确定量子信息理论的结果取决于正半无极锥体的引入正半无极锥体, 并且可以普遍化。 我们展示了Stein的精度和亚麻痹设备属性属性属性属性属性属性的完全共振动程序。 我们展示了Stechin的精度值和亚精度性精度特性, 如果调精度和精度的二次均匀度测量结果都急剧上升, 但是我们向CQQ各州展示了一种可恢复的典型信息。 我们用普通和部分量子值设置的次量子值设置的平行结果, 我们向新的量质质质质测试展示了这个模型的首级的二次曲线结构, 我们用的是超正正正正正正值的次数数据结构的次量值数据序列数据序列模型来显示一个操作框架。 我们也展示了一个普通操作框架, 展示了一个不精确度数据结构。 我们用这个模型展示了一个不全的常规的常规的常规的二次测量的常规操作, 展示了这个实验, 显示一个普通操作的常规操作框架。