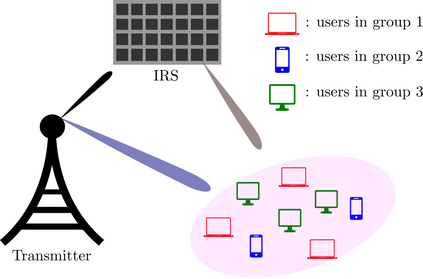
Intelligent reflecting surfaces (IRSs) have shown huge advantages in many potential use cases and thus have been considered a promising candidate for next-generation wireless systems. In this paper, we consider an IRS-assisted multigroup multicast (IRS-MGMC) system in a multiple-input single-output (MISO) scenario, for which the related existing literature is rather limited. In particular, we aim to jointly design the transmit beamformers and IRS phase shifts to maximize the sum rate of the system under consideration. In order to obtain a numerically efficient solution to the formulated non-convex optimization problem, we propose an alternating projected gradient (APG) method where each iteration admits a closed-form and is shown to be superior to a known solution that is derived from the majorization-minimization (MM) method in terms of both achievable sum rate and required complexity, i.e., run time. In particular, we show that the complexity of the proposed APG method grows linearly with the number of IRS tiles, while that of the known solution in comparison grows with the third power of the number of IRS tiles. The numerical results reported in this paper extend our understanding on the achievable rates of large-scale IRS-assisted multigroup multicast systems.
翻译:智能反射表面(IRS)在许多潜在使用案例中显示出巨大的优势,因此被认为是下一代无线系统有希望的候选者。在本文中,我们认为IRS协助的多组多组多功能(IRS-MGMC)系统是一个多投入单产出(MISO)设想方案,对此,有关的现有文献相当有限。特别是,我们的目标是联合设计传输光谱仪和IRS阶段转换,以最大限度地实现所审议系统的总和率。为了从数字上高效率地解决已拟订的非康韦克斯优化问题,我们建议采用一种交替预测梯度(APG)方法,即每个迭代采用封闭式,并显示优于从主要投入-最小化(MIMO)方法得出的已知解决办法,即可实现的总和率和要求的复杂性,即运行时间。我们特别要表明,拟议的APG方法的复杂程度随着IRS小步数的成线性增长,而已知的解决办法则随着我们所了解的可实现的多级IRS系统大规模读取结果的第三强。