Stochastic Primal-Dual Deep Unrolling Networks for Imaging Inverse Problems

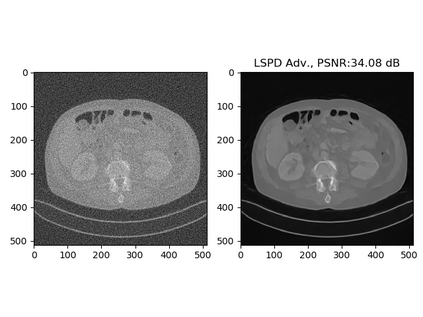
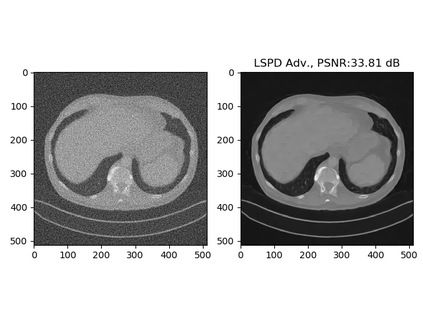
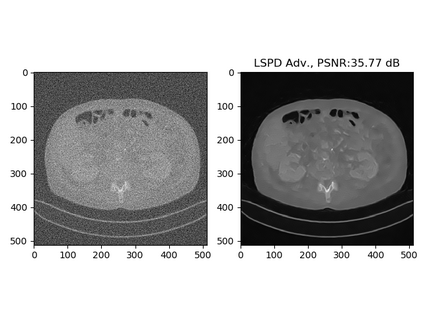
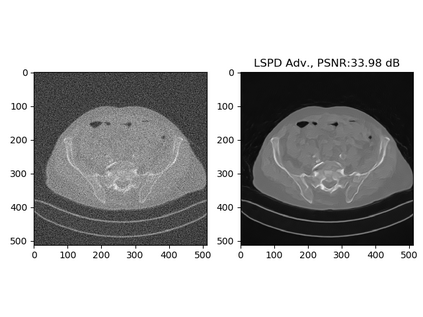
In this work we present a new type of efficient deep-unrolling networks for solving imaging inverse problems. Classical deep-unrolling methods require full forward operator and its adjoint across each layer, and hence can be computationally more expensive than other end-to-end methods such as FBP-ConvNet, especially in 3D image reconstruction tasks. We propose a stochastic (ordered-subsets) extension of the Learned Primal-Dual (LPD) which is the state-of-the-art unrolling network. In our unrolling network, we only use a subset of the forward and adjoint operator, to achieve computational efficiency. We consider 3 ways of training the proposed network to cope with different scenarios of the availability of the training data, including (1) supervised training on paired data, (2) unsupervised adversarial training which enable us to train the network without paired ground-truth data, (3) equivariant self-supervised training approach, which utilizes equivariant structure which is prevalent in many imaging applications, and only requires measurement data. Our numerical results demonstrate the effectiveness of our approach in X-ray CT imaging task, showing that our networks achieve similar reconstruction accuracies as the full-batch LPD, while require only a fraction of the computation.