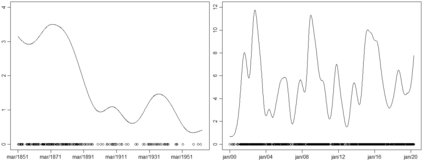
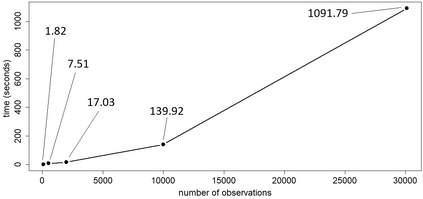
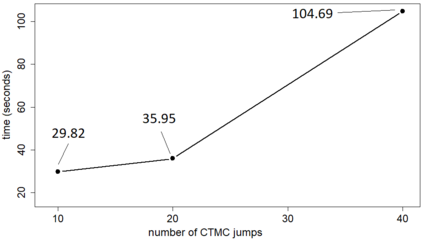
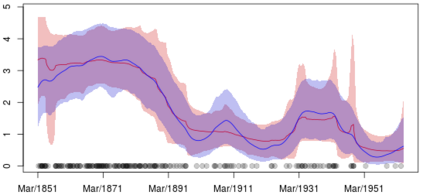
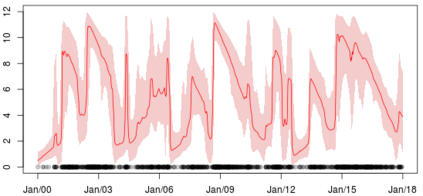
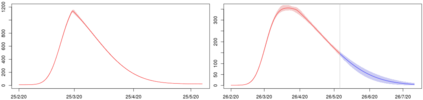
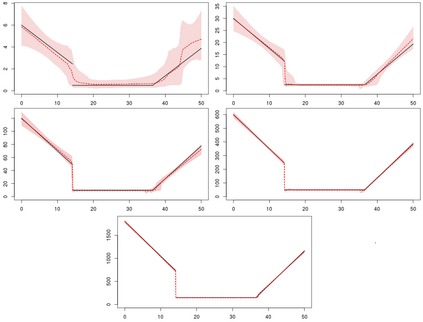
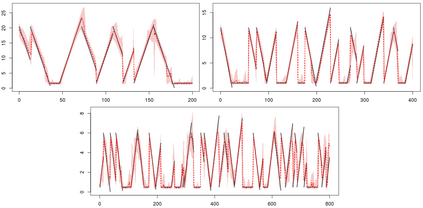
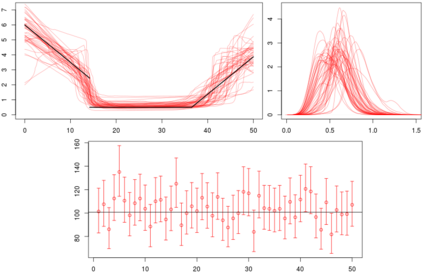
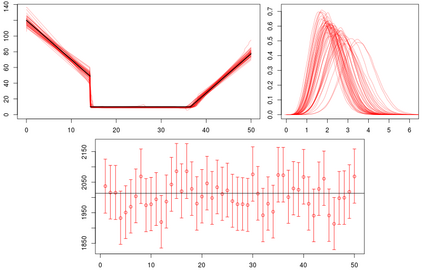
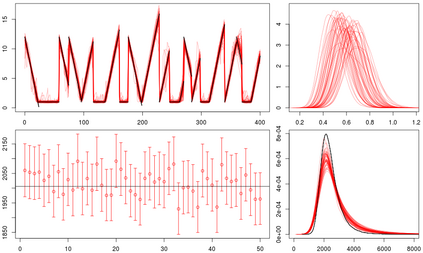
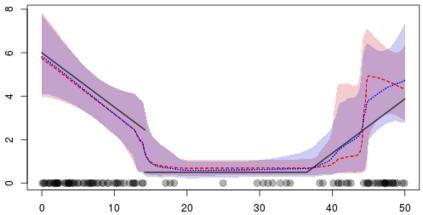
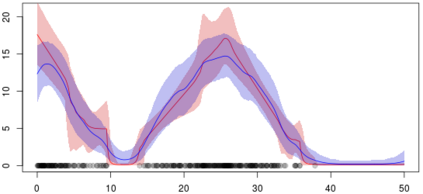
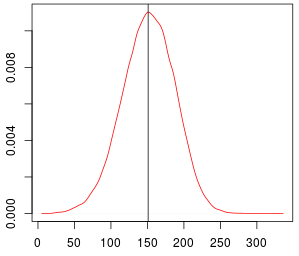
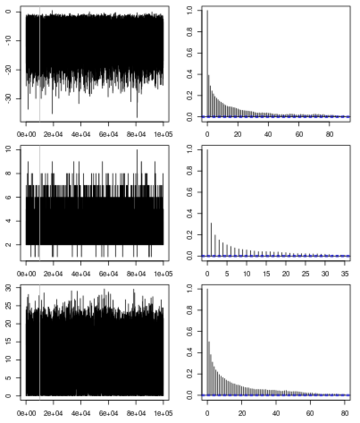
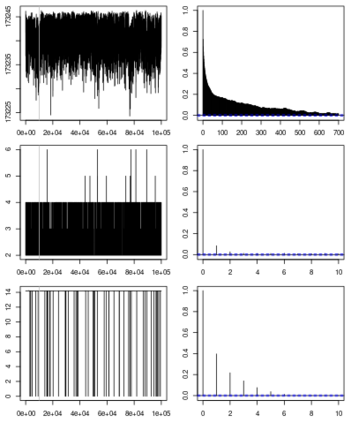
Statistical modeling of point patterns is an important and common problem in several areas. The Poisson process is the most common process used for this purpose, in particular, its generalization that considers the intensity function to be stochastic. This is called a Cox process and different choices to model the dynamics of the intensity gives rise to a wide range of models. We present a new class of unidimensional Cox process models in which the intensity function assumes parametric functional forms that switch among them according to a continuous-time Markov chain. A novel methodology is proposed to perform exact Bayesian inference based on MCMC algorithms. The term exact refers to the fact that no discrete time approximation is used and Monte Carlo error is the only source of inaccuracy. The reliability of the algorithms depends on a variety of specifications which are carefully addressed, resulting in a computationally efficient (in terms of computing time) algorithm and enabling its use with large data sets. Simulated and real examples are presented to illustrate the efficiency and applicability of the proposed methodology. A specific model to fit epidemic curves is proposed and used to analyze data from Dengue Fever in Brazil and COVID-19 in some countries.
翻译:点形的统计模型是几个领域的一个重要和常见的问题。 Poisson 进程是用于此目的的最常见过程,特别是其一般化过程,认为强度函数是随机的。这称为Cox 过程和模型强度动态的不同选择,产生各种各样的模型。我们提出了一个新的单维Cox 过程模型,其强度功能以参数功能形式为新的类别,根据连续时间的Markov 链进行转换。建议采用新的方法,根据MCMC算法进行精确的Bayesian推论。该术语准确指没有使用离散时间近似,而Monte Carlo错误是不准确的唯一来源。算法的可靠性取决于各种规格,这些规格经过仔细处理,从而产生一种高效的计算(计算时间)算法,并能够用大型数据集加以使用。模拟和真实的例子说明拟议方法的效率和适用性。提出了适合巴西Dengue Fever和一些COVID-19国家数据的具体模型。