Consistency of common spatial estimators under spatial confounding

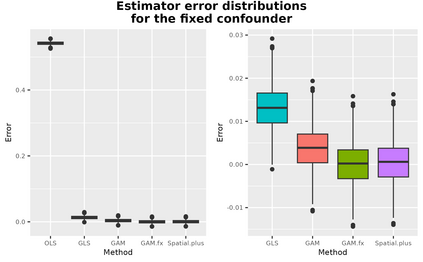
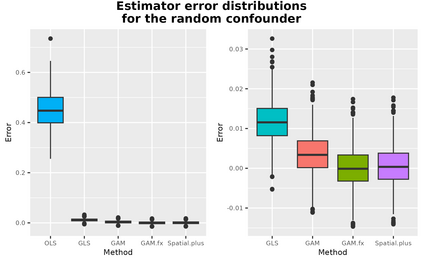
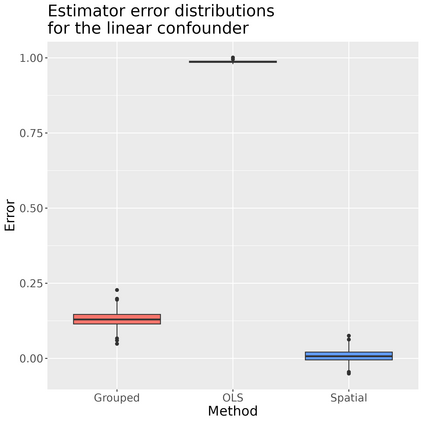
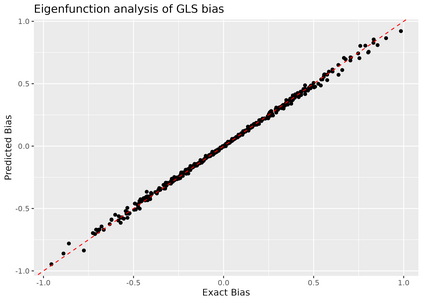
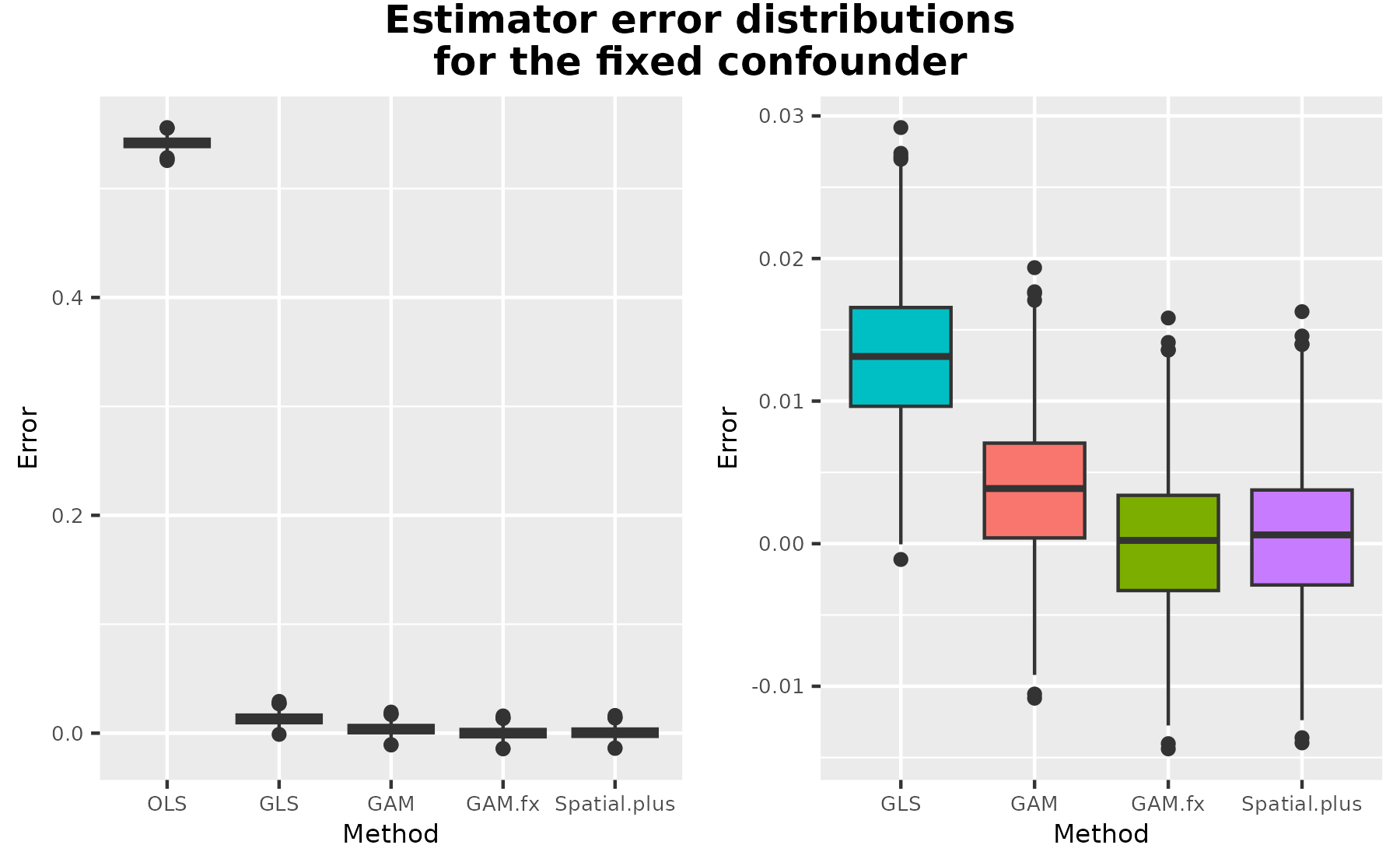
This paper addresses the asymptotic performance of popular spatial regression estimators on the task of estimating the effect of an exposure on an outcome in the presence of an unmeasured spatially-structured confounder. This setting is often referred to as "spatial confounding." We consider spline models, Gaussian processes (GP), generalized least squares (GLS), and restricted spatial regression (RSR) under two data generation processes: one where the confounder is a fixed effect and one where it is a random effect. The literature on spatial confounding is confusing and contradictory, and our results correct and clarify several misunderstandings. We first show that, like an unadjusted OLS estimator, RSR is asymptotically biased under any spatial confounding scenario. We then prove a novel result on the consistency of the GLS estimator under spatial confounding. We finally prove that estimators like GLS, GP, and splines, that are consistent under confounding by a fixed effect will also be consistent under confounding by a random effect. We conclude that, contrary to much of the recent literature on spatial confounding, traditional estimators based on partially linear models are amenable to estimating effects in the presence of spatial confounding. We support our theoretical arguments with simulation studies.