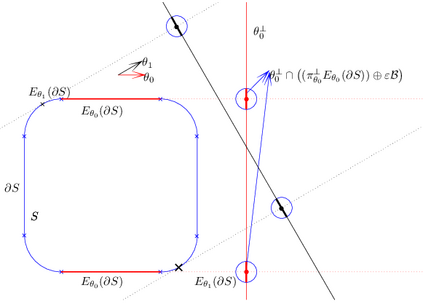
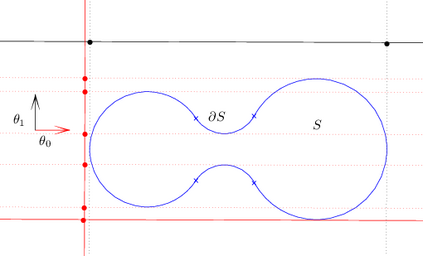
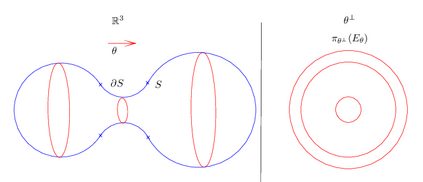
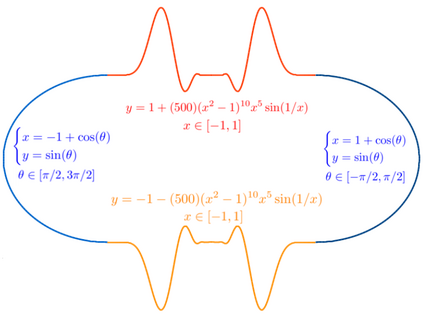
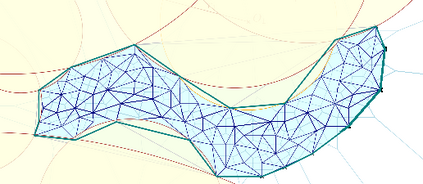
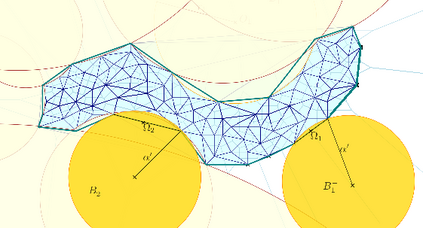
We study the problem of estimating the surface area of the boundary $\partial S$ of a sufficiently smooth set $S\subset\mathbb{R}^d$ when the available information is only a finite subset $\X\subset S$. We propose two estimators. The first makes use of the Devroye--Wise support estimator and is based on Crofton's formula, which, roughly speaking, states that the $(d-1)$-dimensional surface area of a smooth enough set is the mean number of intersections of randomly chosen lines. For that purpose, we propose an estimator of the number of intersections of such lines with support based on the Devroye--Wise support estimators. The second surface area estimator makes use of the $\alpha$-convex hull of $\X$, which is denoted by $C_{\alpha}(\X)$. More precisely, it is the $(d-1)$-dimensional surface area of $C_\alpha(\X)$, as denoted by $|C_\alpha(\X)|_{d-1}$, which is proven to converge to the $(d-1)$-dimensional surface area of $\partial S$. Moreover, $|C_\alpha(\X)|_{d-1}$ can be computed using Crofton's formula. Our results depend on the Hausdorff distance between $S$ and $\X$ for the Devroye--Wise estimator, and the Hausdorff distance between $\partial S$ and $\partial C_{\alpha}(\X)$ for the second estimator.
翻译:我们研究如何估算边界的表面面积 $\ efe- Wise 支持估测器。 我们首先使用 Devroye- Wise 支持估测器, 并以克罗福顿公式为基础, 粗略地说, 平滑的一组表示 $( d-1) 的表面面积是随机选择的线条的中间点的平均值。 为此, 我们提议在基于 Devroye- Wize 支持估测器的支持下估算这些线条的交叉点的数量。 第二个表面积使用 $\ al- Wise 支持估测器 $\ Xx美元, 以 美元表示 =alpha} (d-1) 美元 平滑的表面面积是 $( d-1) 美元, 随机选择的直径是 $( X) 美元 和 美元 美元。 直径(x) 直径(x) 和直径(x) 美元) 直径(xx- 美元) 和直径(xx=xxx) 美元) 美元。