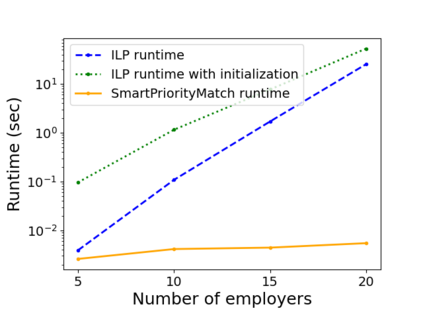
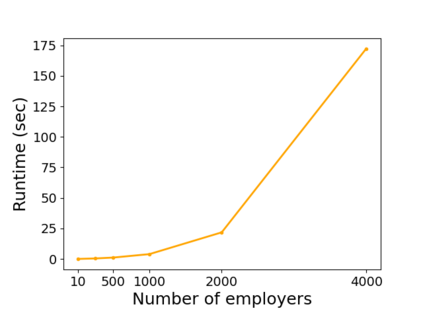
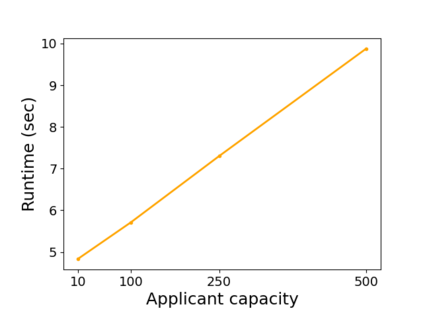
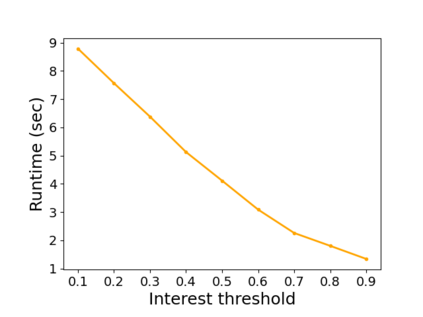
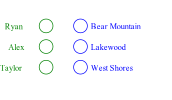
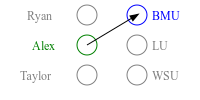
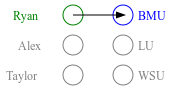
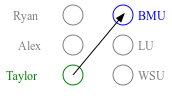
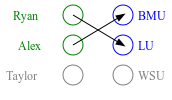
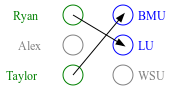
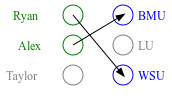
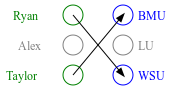
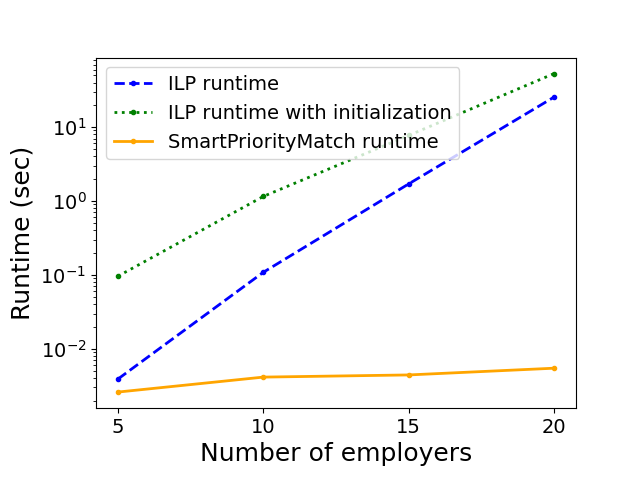
While the stable marriage problem and its variants model a vast range of matching markets, they fail to capture complex agent relationships, such as the affiliation of applicants and employers in an interview marketplace. To model this problem, the existing literature on matching with externalities permits agents to provide complete and total rankings over matchings based off of both their own and their affiliates' matches. This complete ordering restriction is unrealistic, and further the model may have an empty core. To address this, we introduce the Dichotomous Affiliate Stable Matching (DASM) Problem, where agents' preferences indicate dichotomous acceptance or rejection of another agent in the marketplace, both for themselves and their affiliates. We also assume the agent's preferences over entire matchings are determined by a general weighted valuation function of their (and their affiliates') matches. Our results are threefold: (1) we use a human study to show that real-world matching rankings follow our assumed valuation function; (2) we prove that there always exists a stable solution by providing an efficient, easily-implementable algorithm that finds such a solution; and (3) we experimentally validate the efficiency of our algorithm versus a linear-programming-based approach.
翻译:虽然稳定的婚姻问题及其变式模式模拟了广泛的匹配市场,但是它们未能捕捉复杂的代理关系,例如申请人和雇主在面试市场中的附属关系。为模拟这一问题,关于与外部性匹配的现有文献允许代理商根据自己的和子公司之间的匹配提供完整和总的排名。这种完整的定购限制是不现实的,而且模型可能有一个空核心。为了解决这个问题,我们引入了Dicotomous Affiliate Settle Confirming (DASM) 问题, 代理商的偏好表明市场中另一代理商的分母接受或拒绝, 包括他们本人和他们的子公司。 我们还假设代理商对全部匹配的偏好是由他们( 及其子公司) 匹配的一般加权估值功能决定的。 我们的结果有三重:(1) 我们使用人类研究来表明真实世界的匹配排序与我们假设的估值功能相仿;(2) 我们证明,通过提供一种高效、易于实施的算法,找到这样的解决办法, 总是有稳定的解决方案;(3) 我们实验性地验证我们的算法相对于线性方法的效率。