Optimal Convergence Rate of Lie-Trotter Approximation for Quantum Thermal Averages

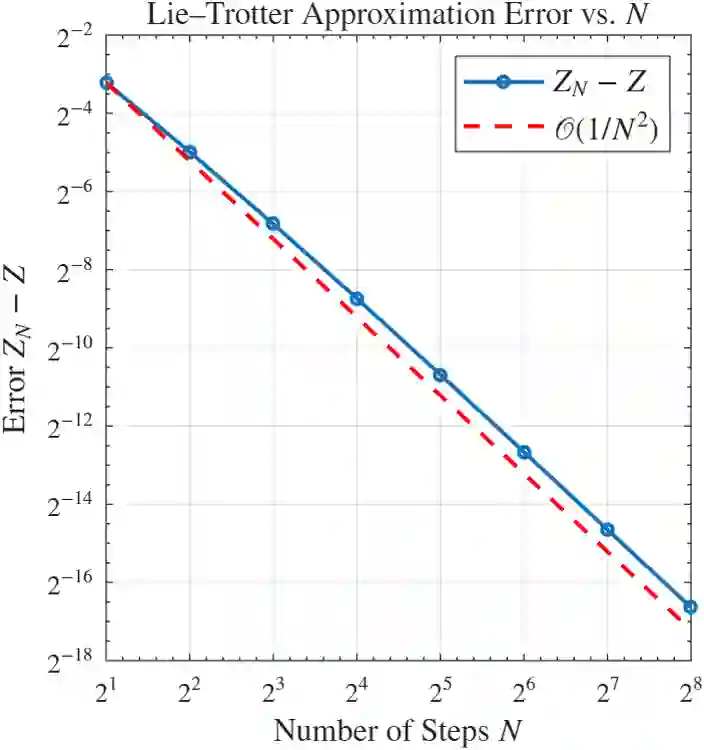
The Lie--Trotter product formula is a foundational approximation for the quantum partition function, yet obtaining rigorous error bounds for the unbounded Hamiltonians common in physics remains a significant challenge. This paper provides a quantitative error analysis for this approximation across two key systems. For a particle in a smooth, periodic potential, we establish an optimal convergence rate of $\mathcal O(1/N^2)$ for both the partition function and thermal averages, where $N$ is the number of imaginary time steps. We then extend this analysis to the more challenging case of a confining potential on $\mathbb R$, proving a nearly optimal rate of $\mathcal O((\log N+1)^{\frac32}/N^2)$. The derived error bounds provide a firm mathematical foundation for the high-order accuracy of path integral simulations in quantum statistical mechanics.