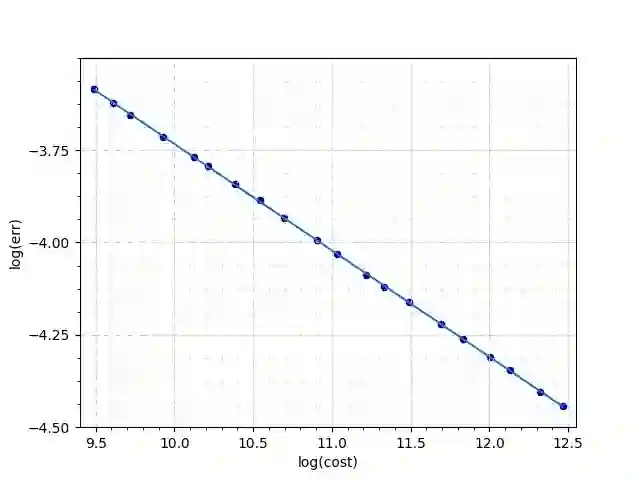
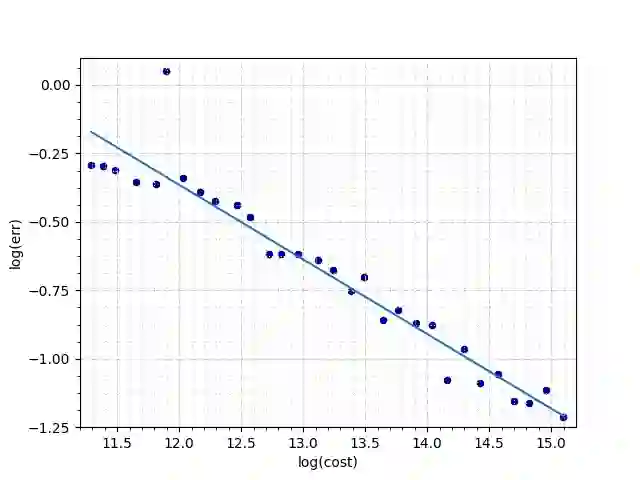
In this paper we deal with pointwise approximation of solutions of stochastic differential equations (SDEs) driven by infinite dimensional Wiener process with additional jumps generated by Poisson random measure. The further investigations contain upper error bounds for the proposed truncated dimension randomized Euler scheme. We also establish matching (up to constants) upper and lower bounds for $\varepsilon$-complexity and show that the defined algorithm is optimal in the Information-Based Complexity (IBC) sense. Finally, results of numerical experiments performed by using GPU architecture are also reported.
翻译:在本文中,我们处理的是由无限维纳进程驱动的随机跳跃式差异方程式(SDEs)解决方案的近似点。 进一步的调查包含拟议短线尺寸随机变电法计划的上误差界限。 我们还为$\varepsilon$- complexity 建立匹配( 最高为常数), 并显示定义的算法在基于信息的复杂度( IBC) 的意义上是最佳的。 最后, 也报告了使用 GPU 结构进行的数字实验的结果 。