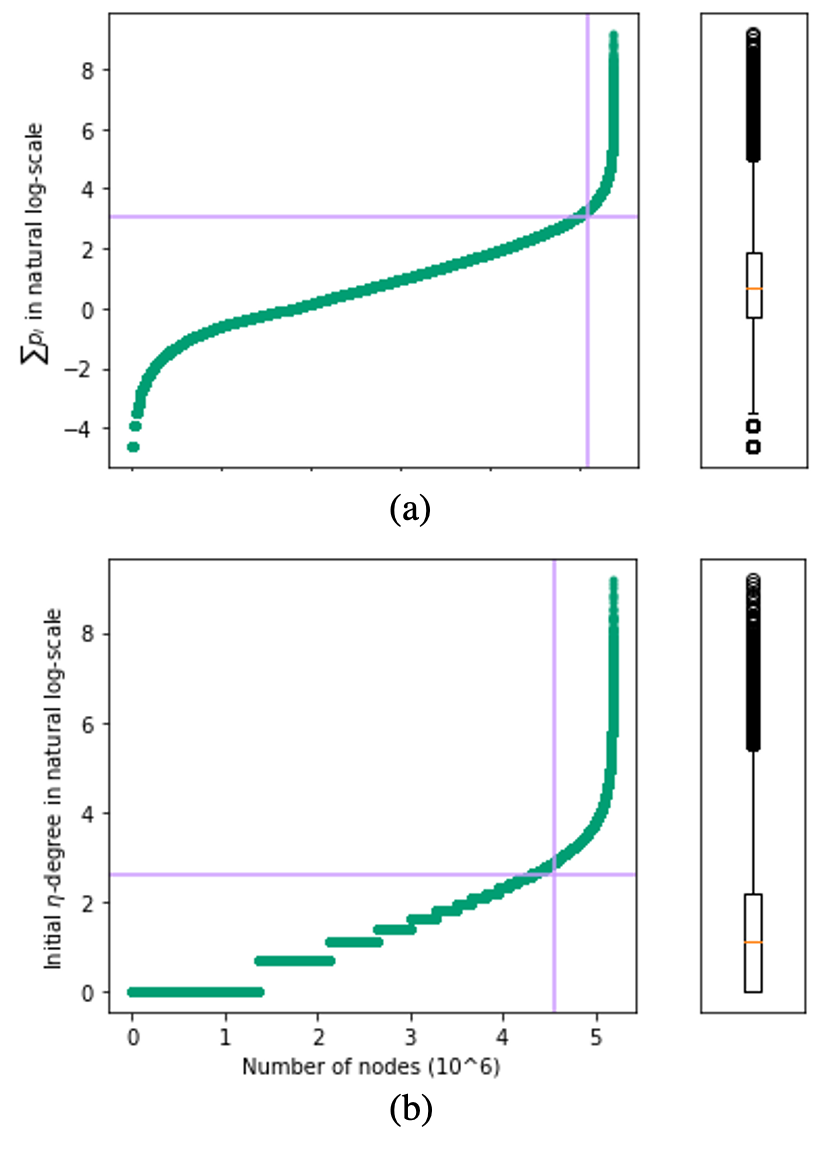
Mining dense subgraphs where vertices connect closely with each other is a common task when analyzing graphs. A very popular notion in subgraph analysis is core decomposition. Recently, Esfahani et al. presented a probabilistic core decomposition algorithm based on graph peeling and Central Limit Theorem (CLT) that is capable of handling very large graphs. Their proposed peeling algorithm (PA) starts from the lowest degree vertices and recursively deletes these vertices, assigning core numbers, and updating the degree of neighbour vertices until it reached the maximum core. However, in many applications, particularly in biology, more valuable information can be obtained from dense sub-communities and we are not interested in small cores where vertices do not interact much with others. To make the previous PA focus more on dense subgraphs, we propose a multi-stage graph peeling algorithm (M-PA) that has a two-stage data screening procedure added before the previous PA. After removing vertices from the graph based on the user-defined thresholds, we can reduce the graph complexity largely and without affecting the vertices in subgraphs that we are interested in. We show that M-PA is more efficient than the previous PA and with the properly set filtering threshold, can produce very similar if not identical dense subgraphs to the previous PA (in terms of graph density and clustering coefficient).
翻译:在分析图表时,一个常见的任务就是将脊椎紧密地连接在一起的采矿密集的子图层。在子图分析中,一个非常流行的概念是核心分解。最近,Esfahani等人根据图形剥皮和中央限制理论(CLT),提出了一个能够处理大图的概率核心分解算法。他们提议的剥离算法(PA)从最低程度的脊椎开始,反复删除这些脊椎,分配核心数字,更新邻居的脊椎程度,直到它达到最大核心。然而,在许多应用中,特别是生物学应用中,可以从密集的子群中获取更有价值的信息,而我们对于小块核心不感兴趣的核心分解算法(CLT ) 能够处理非常大的图表。为了让先前的脊椎更加集中,我们建议一个多阶段的剖析算法(M-PA), 在根据用户定义的临界值从图表中去除了两个阶段的数据筛选程序之后,我们可以从图表中去除更多的脊椎,我们不会在先前的底线上,我们也可以用更深的底的底的底线线,我们可以用的底图来降低的精度。