Design and Analysis of Switchback Experiments

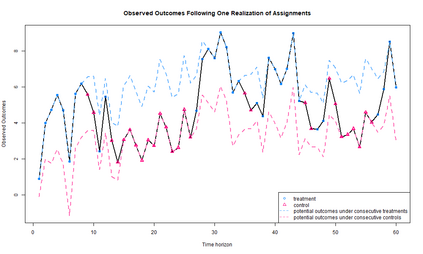
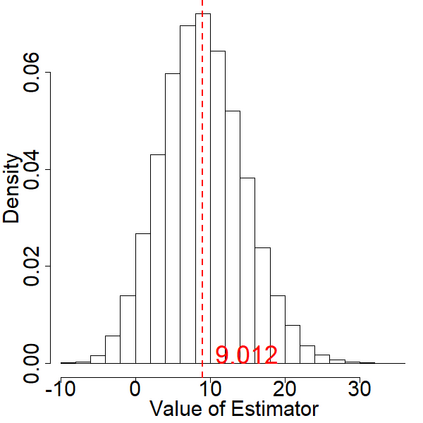
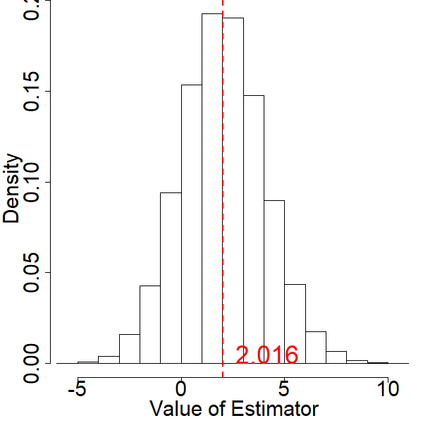
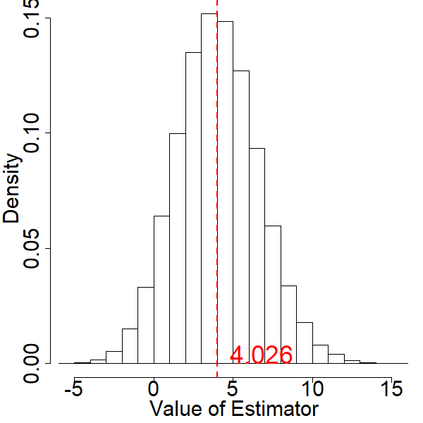
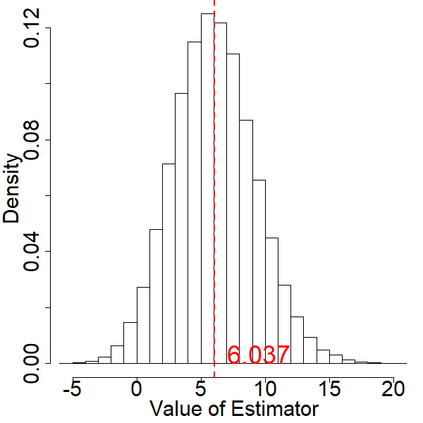
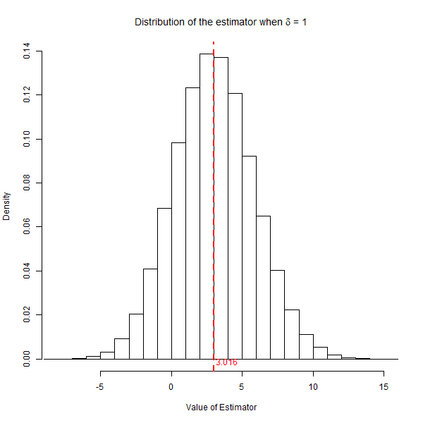
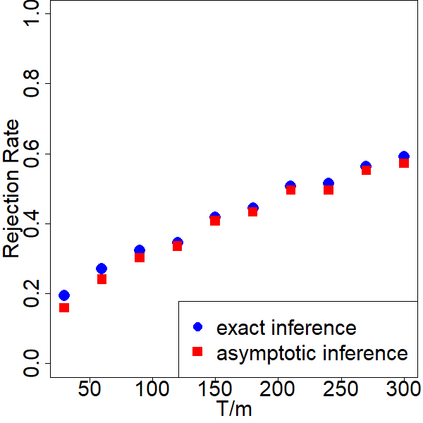
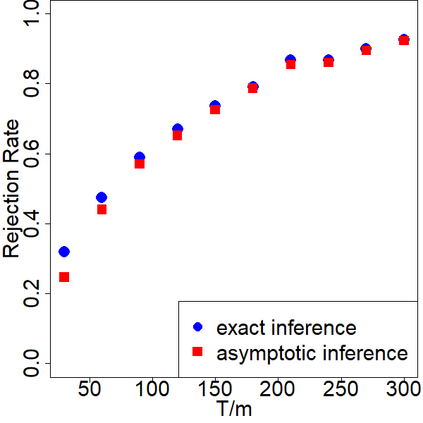
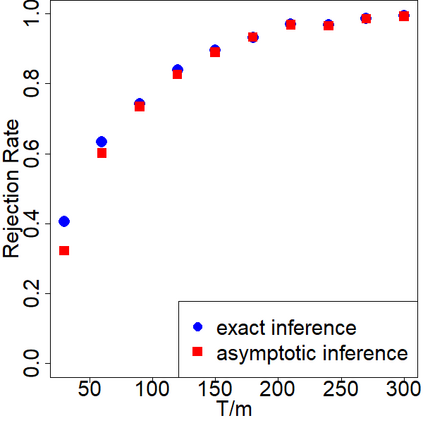
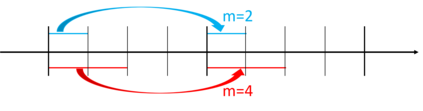
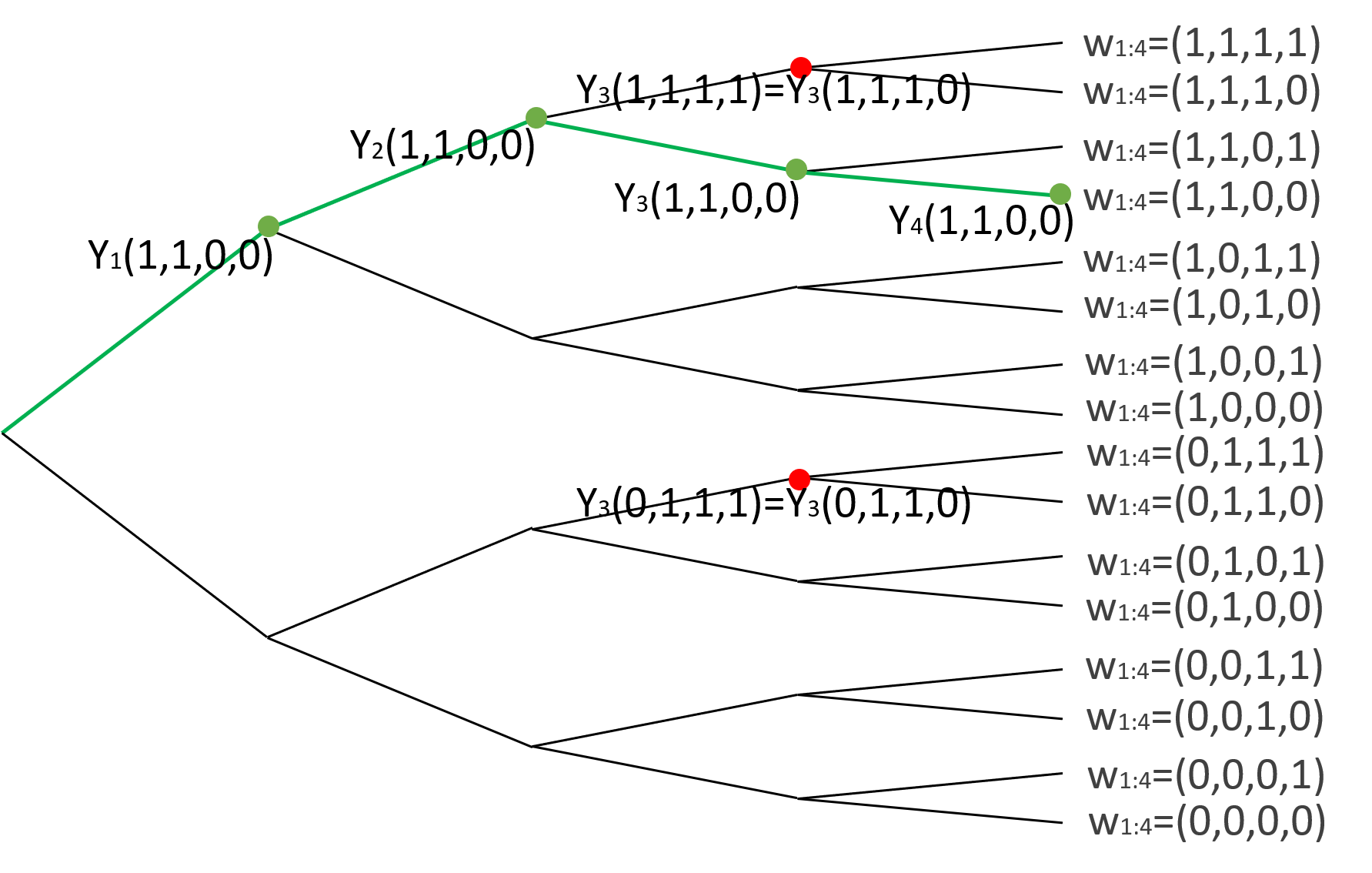
In switchback experiments, a firm sequentially exposes an experimental unit to a random treatment, measures its response, and repeats the procedure for several periods to determine which treatment leads to the best outcome. Although practitioners have widely adopted this experimental design technique, the development of its theoretical properties and the derivation of optimal design procedures have been, to the best of our knowledge, elusive. In this paper, we address these limitations by establishing the necessary results to ensure that practitioners can apply this powerful class of experiments with minimal assumptions. Our main result is the derivation of the optimal design of switchback experiments under a range of different assumptions on the order of carryover effect - that is, the length of time a treatment persists in impacting the outcome. We cast the experimental design problem as a minimax discrete robust optimization problem, identify the worst-case adversarial strategy, establish structural results for the optimal design, and finally solve the problem via a continuous relaxation. For the optimal design, we derive two approaches for performing inference after running the experiment. The first provides exact randomization based $p$-values and the second uses a finite population central limit theorem to conduct conservative hypothesis tests and build confidence intervals. We further provide theoretical results for our inferential procedures when the order of the carryover effect is misspecified. For firms that possess the capability to run multiple switchback experiments, we also provide a data-driven strategy to identify the likely order of carryover effect. To study the empirical properties of our results, we conduct extensive simulations. We conclude the paper by providing some practical suggestions.