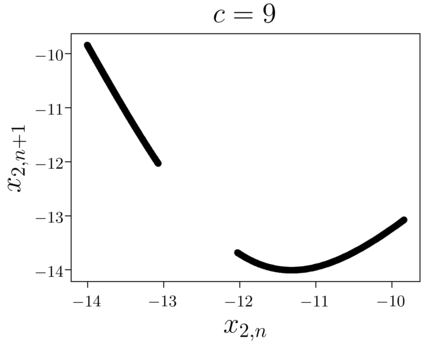
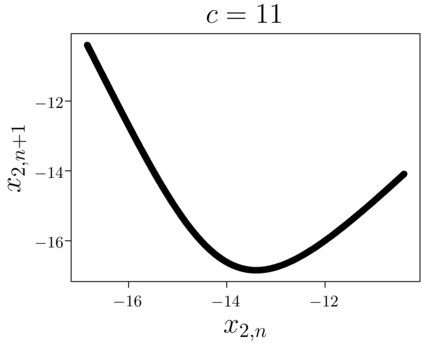
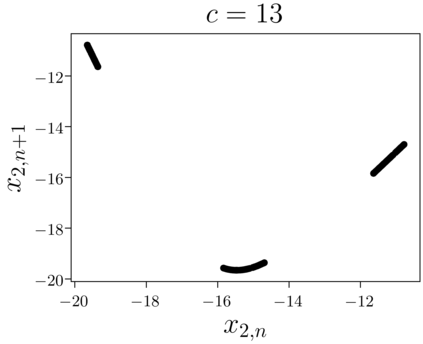
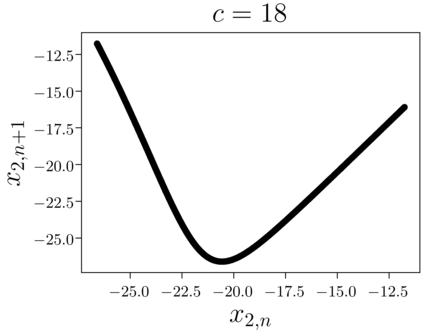
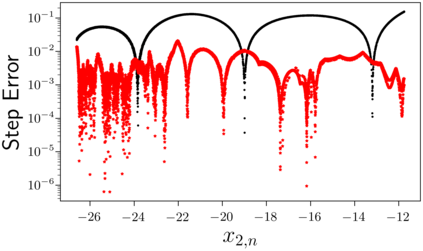
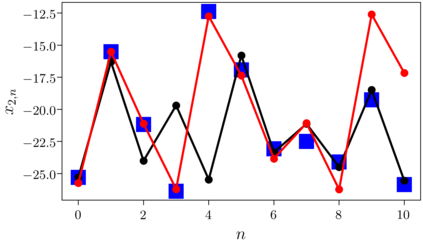
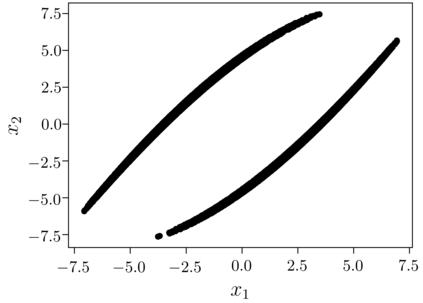
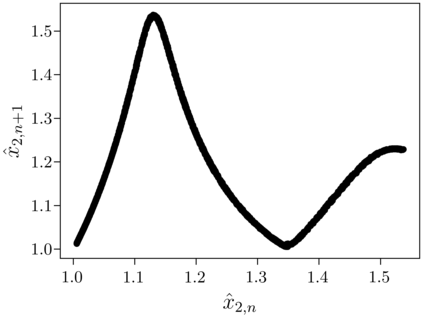
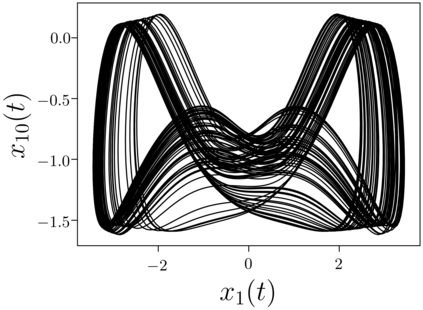
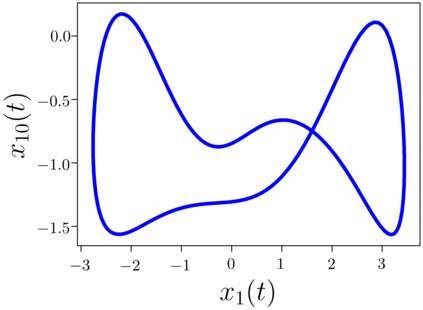
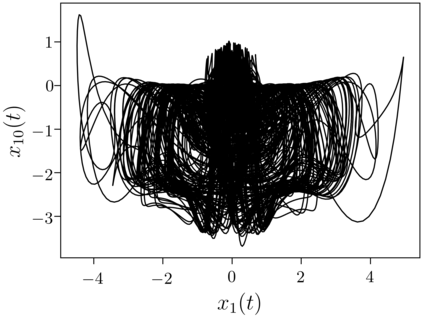
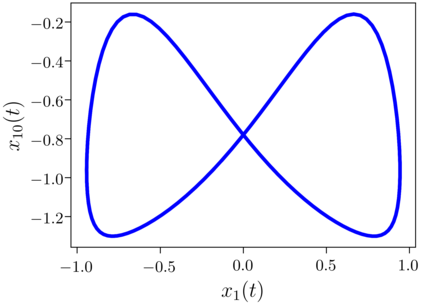
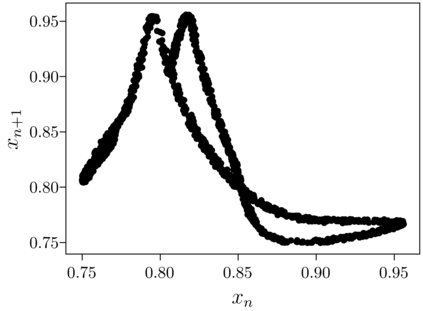
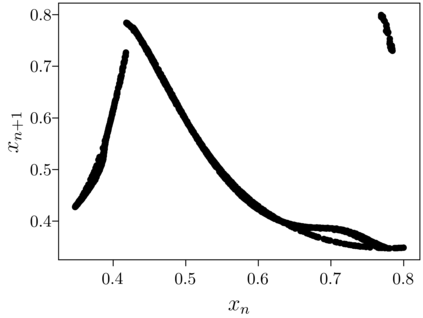
Despite many of the most common chaotic dynamical systems being continuous in time, it is through discrete time mappings that much of the understanding of chaos is formed. Henri Poincar\'e first made this connection by tracking consecutive iterations of the continuous flow with a lower-dimensional, transverse subspace. The mapping that iterates the dynamics through consecutive intersections of the flow with the subspace is now referred to as a Poincar\'e map, and it is the primary method available for interpreting and classifying chaotic dynamics. Unfortunately, in all but the simplest systems, an explicit form for such a mapping remains outstanding. This work proposes a method for obtaining explicit Poincar\'e mappings by using deep learning to construct an invertible coordinate transformation into a conjugate representation where the dynamics are governed by a relatively simple chaotic mapping. The invertible change of variable is based on an autoencoder, which allows for dimensionality reduction, and has the advantage of classifying chaotic systems using the equivalence relation of topological conjugacies. Indeed, the enforcement of topological conjugacies is the critical neural network regularization for learning the coordinate and dynamics pairing. We provide expository applications of the method to low-dimensional systems such as the R\"ossler and Lorenz systems, while also demonstrating the utility of the method on infinite-dimensional systems, such as the Kuramoto--Sivashinsky equation.
翻译:尽管许多最常见的混乱动态系统在时间上是连续的,但正是通过离散的时间绘图,才形成了对混乱的大部分理解。Henri Poincar\'e首先通过跟踪连续循环,以低维、反向的子空间跟踪连续流动的连续循环。通过与亚空间流动的连续交叉循环动态的绘图现在被称为Poincar\'e地图,这是解释和分类混乱动态的主要方法。不幸的是,在所有简单系统之外,这种绘图的明确形式仍然悬而未决。这项工作提出一种方法,通过利用深层学习,构建不可逆的坐标转换为共振动代表,使动态受到相对简单的混乱映射的调节。变量的不可置疑变化以自动编码为基础,它能够降低维度,并且具有利用等同性结构组合关系对混乱系统进行分类的优势。事实上,顶端相纠结的调和调控式系统是关键的内基网络,同时学习调和调控式系统,作为我们调和演化的平流式系统。