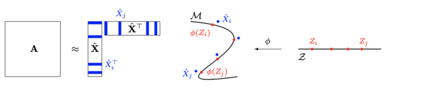
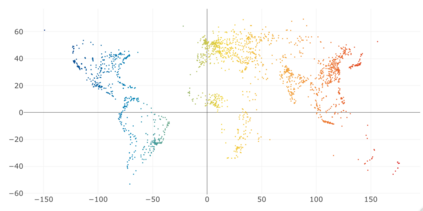
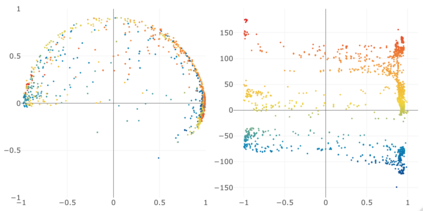
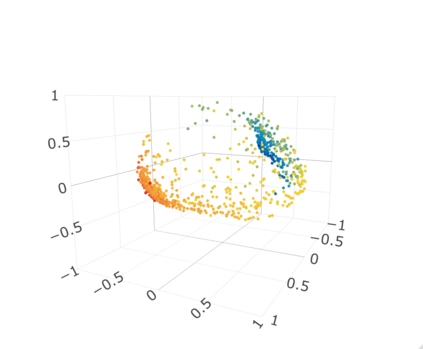
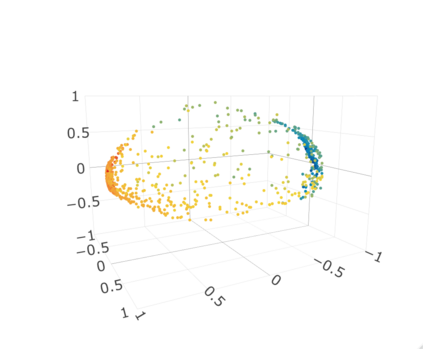
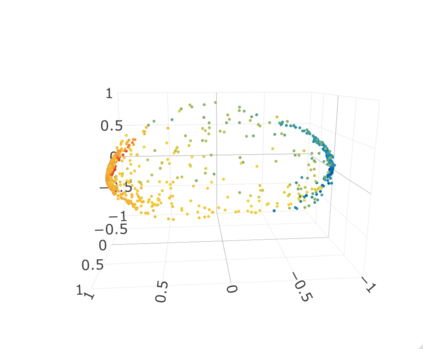
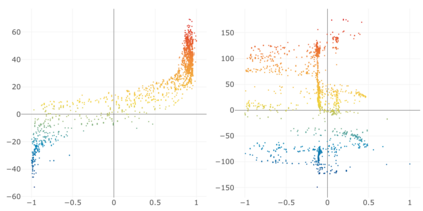
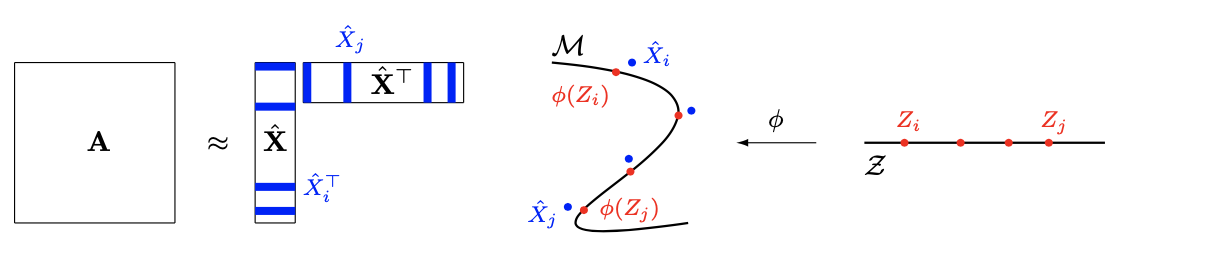
Given a graph or similarity matrix, we consider the problem of recovering a notion of true distance between the nodes, and so their true positions. Through new insights into the manifold geometry underlying a generic latent position model, we show that this can be accomplished in two steps: matrix factorisation, followed by nonlinear dimension reduction. This combination is effective because the point cloud obtained in the first step lives close to a manifold in which latent distance is encoded as geodesic distance. Hence, a nonlinear dimension reduction tool, approximating geodesic distance, can recover the latent positions, up to a simple transformation. We give a detailed account of the case where spectral embedding is used, followed by Isomap, and provide encouraging experimental evidence for other combinations of techniques.
翻译:根据图表或类似的矩阵,我们考虑的是恢复节点之间真实距离概念的问题,也就是其真实位置的问题。通过对通用潜伏位置模型的多重几何学进行新的洞察,我们表明这可以分两个步骤实现:矩阵乘数化,然后是非线性维度的减少。这种结合是有效的,因为第一步获得的点云接近一个将潜在距离编码为大地测量距离的方块。因此,一个非线性维度减少工具,近似大地测量距离,可以恢复潜伏位置,直至简单转变。我们详细介绍了光谱嵌入的情况,然后是伊索马普,并为其他技术组合提供令人鼓舞的实验证据。