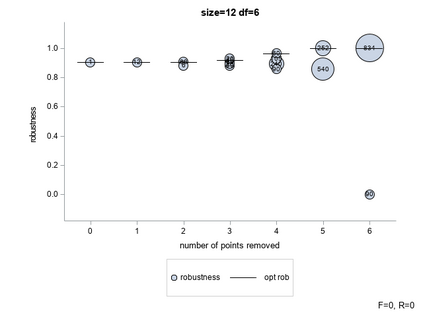
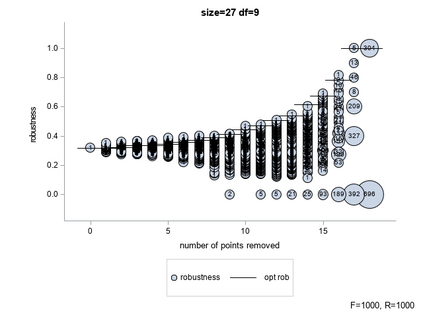
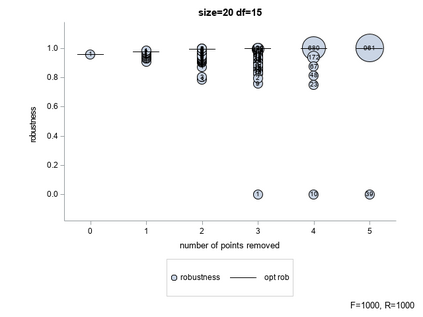
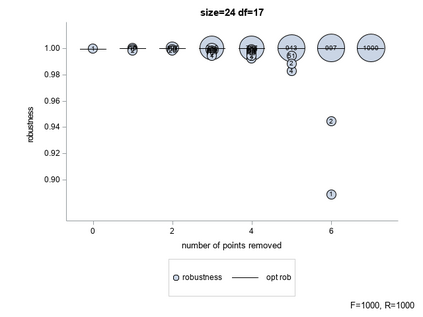
The paper describes an algorithm that, given an initial design $\mathcal{F}_n$ of size $n$ and a linear model with $p$ parameters, provides a sequence $\mathcal{F}_n \supset \ldots \supset \mathcal{F}_{n-k} \supset \ldots \supset \mathcal{F}_p$ of nested \emph{robust} designs. The sequence is obtained by the removal, one by one, of the runs of $\mathcal{F}_n$ till a $p$-run \emph{saturated} design $\mathcal{F}_p$ is obtained. The potential impact of the algorithm on real applications is high. The initial fraction $\mathcal{F}_n$ can be of any type and the output sequence can be used to organize the experimental activity. The experiments can start with the runs corresponding to $\mathcal{F}_p$ and continue adding one run after the other (from $\mathcal{F}_{n-k}$ to $\mathcal{F}_{n-k+1}$) till the initial design $\mathcal{F}_n$ is obtained. In this way, if for some unexpected reasons the experimental activity must be stopped before the end when only $n-k$ runs are completed, the corresponding $\mathcal{F}_{n-k}$ has a high value of robustness for $k \in \{1, \ldots, n-p\}$. The algorithm uses the circuit basis, a special representation of the kernel of a matrix with integer entries. The effectiveness of the algorithm is demonstrated through the use of simulations.
翻译:纸张描述的算法,根据初始设计 $\ mathcal{F\\\\\ 美元大小的美元和一个带有美元参数的线性模型,提供序列 $mathcal{F\\\ n\\\\ supset\ mathcal{F\\\\\ n\\\ k}\\\ supcal{F\\\\\\\\\ k} 这样的算法,在初始设计设计 $\ mathcal{F\\\\\\\\ f\\\ p} 中, 排序通过清除获得, 逐个运出 $mathcal{fn\\\\\\ nF\\\\\\\\ n美元运行到美元运行 美元运行到美元运行 美元运行。 在初始设计之前, 算入 。 运算的最初部分 $\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\