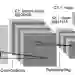
In this paper, we consider the problem of binary classification with a class of general deep convolutional neural networks, which includes fully-connected neural networks and fully convolutional neural networks as special cases. We establish non-asymptotic excess risk bounds for a class of convex surrogate losses and target functions with different modulus of continuity. An important feature of our results is that we clearly define the prefactors of the risk bounds in terms of the input data dimension and other model parameters and show that they depend polynomially on the dimensionality in some important models. We also show that the classification methods with CNNs can circumvent the curse of dimensionality if the input data is supported on an approximate low-dimensional manifold. To establish these results, we derive an upper bound for the covering number for the class of general convolutional neural networks with a bias term in each convolutional layer, and derive new results on the approximation power of CNNs for any uniformly-continuous target functions. These results provide further insights into the complexity and the approximation power of general convolutional neural networks, which are of independent interest and may have other applications. Finally, we apply our general results to analyze the non-asymptotic excess risk bounds for four widely used methods with different loss functions using CNNs, including the least squares, the logistic, the exponential and the SVM hinge losses.
翻译:在本文中,我们考虑的是一个二进制分类问题,即一个总体深深层神经神经神经网络,包括完全连接的神经网络和完全进化的神经网络的二进制分类问题,它包括完全连接的神经网络和完全进化的神经网络,作为特例。我们为一组 convex 替代损失和具有不同连续性模数的目标功能,建立了非无线过度的风险圈。我们结果的一个重要特征是,我们从输入数据维度和其他模型参数的角度明确界定风险界限的前导因素,并表明它们多在多个重要模型的维度上依赖多种形式。我们还表明,如果输入数据在大约一个低维度的多元方面得到支持,CNN的分类方法可以绕过维度的诅咒。为了确定这些结果,我们为一般革命神经网络的覆盖数量定了一个上限,每个革命层都有偏差术语,并且从CNN的近功率中得出新的结果,表明它们取决于某些重要模型的维度。这些结果进一步揭示了普通革命神经网络的复杂性和近度能力,包括使用四种不同层次的逻辑结果,最后是使用不同的方式分析。