Energy contraction and optimal convergence of adaptive iterative linearized finite element methods

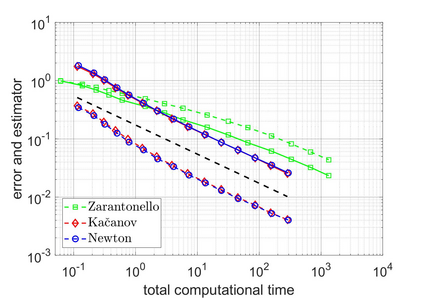
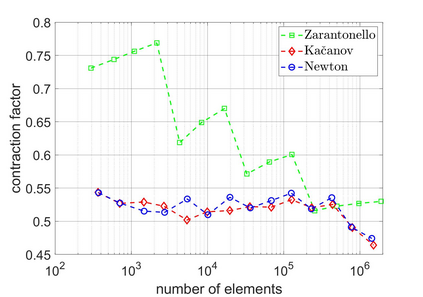
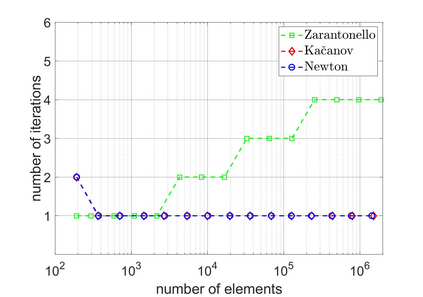
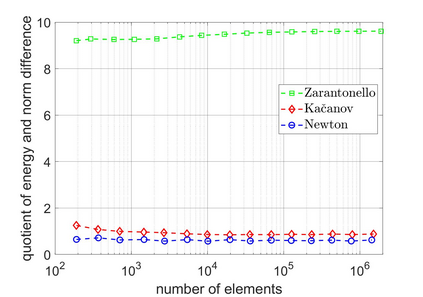
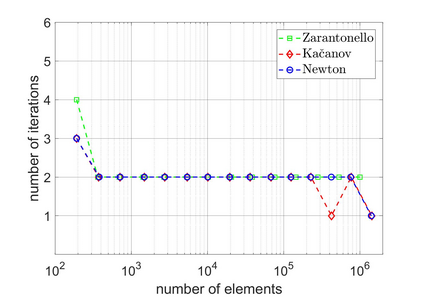
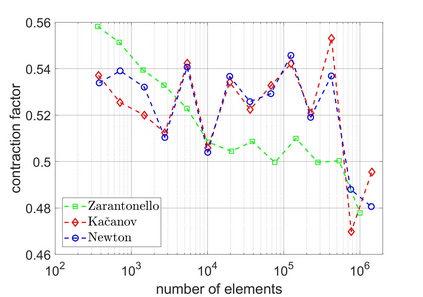
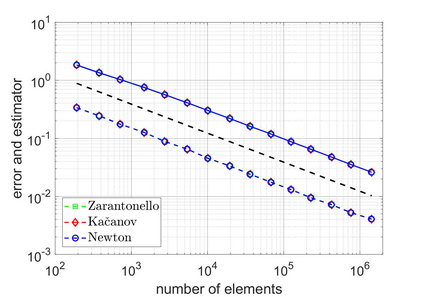
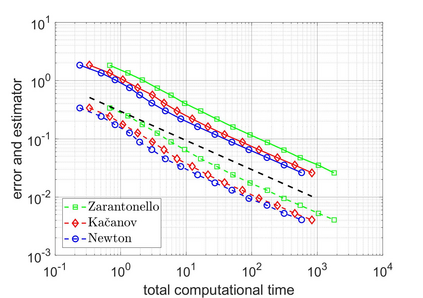
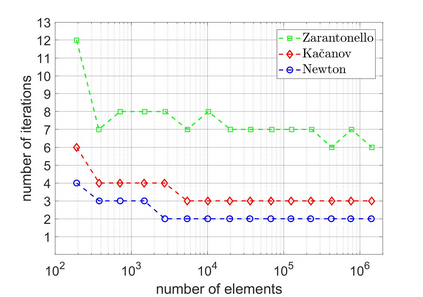
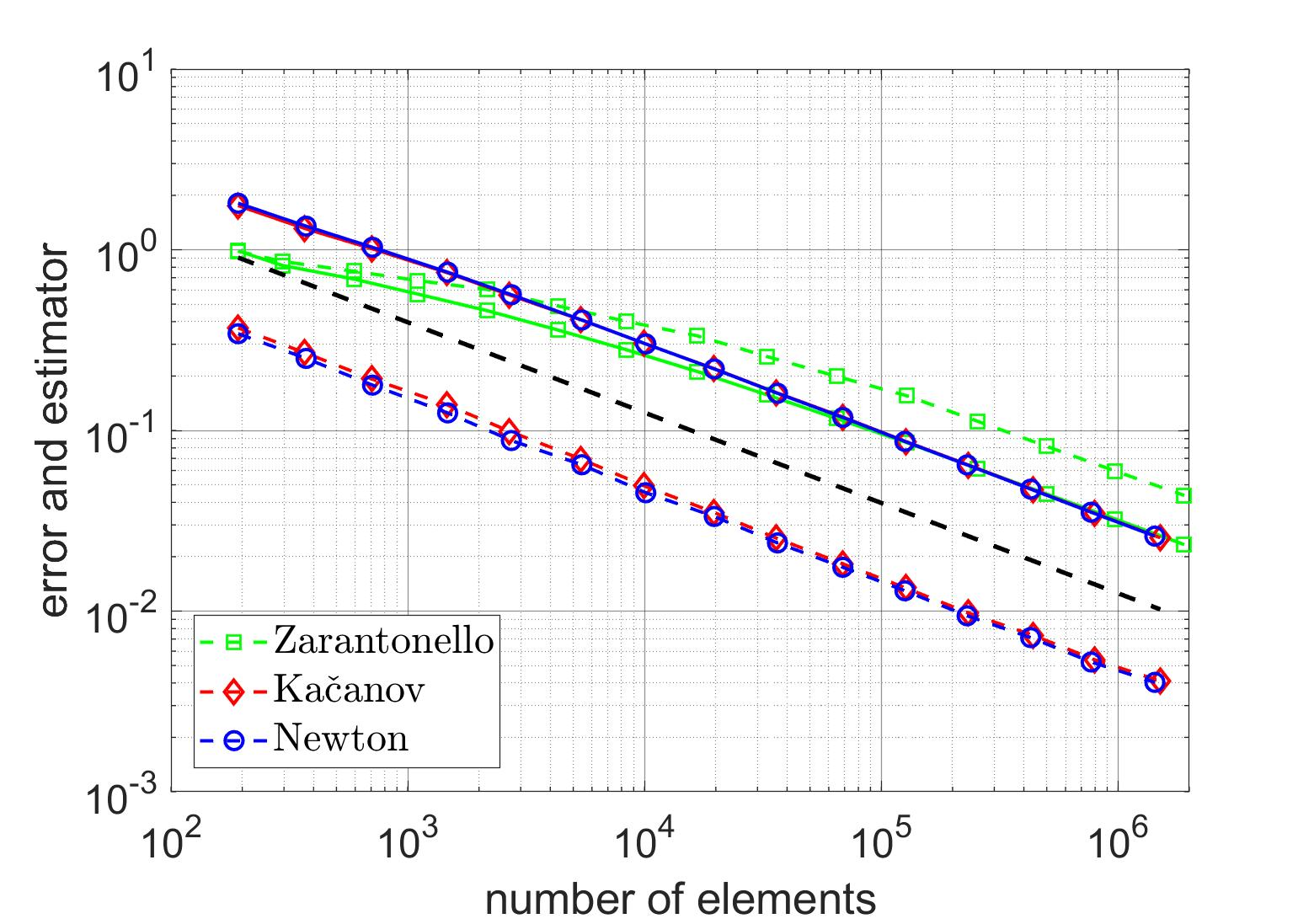
We revisit a unified methodology for the iterative solution of nonlinear equations in Hilbert spaces. Our key observation is that the general approach from [Heid & Wihler, Math. Comp. 89 (2020), Calcolo 57 (2020)] satisfies an energy contraction property in the context of (abstract) strongly monotone problems. This property, in turn, is the crucial ingredient in the recent convergence analysis in [Gantner et al., arXiv:2003.10785]. In particular, we deduce that adaptive iterative linearized finite element methods (AILFEMs) lead to full linear convergence with optimal algebraic rates with respect to the degrees of freedom as well as the total computational time.