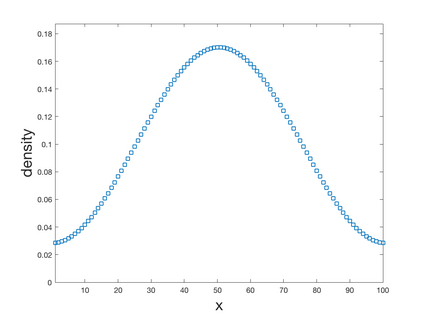
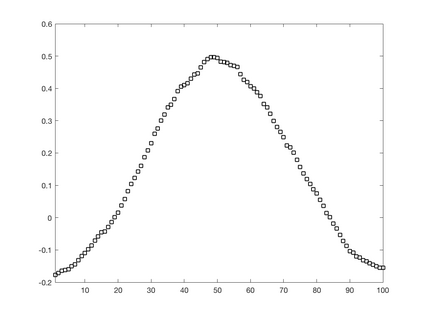
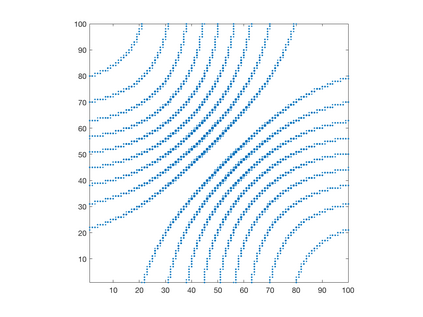
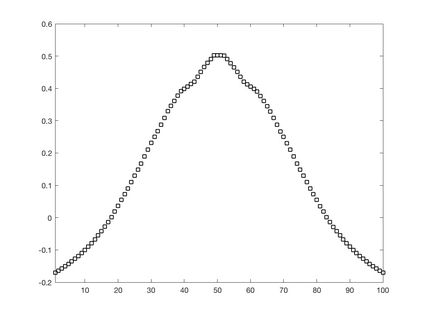
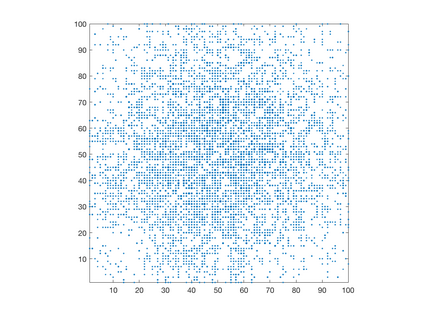
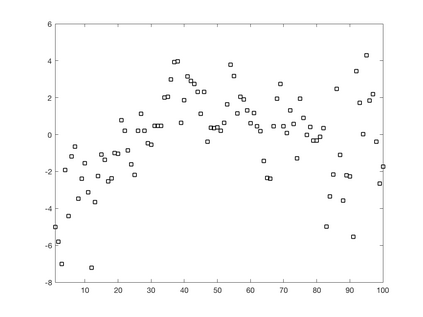
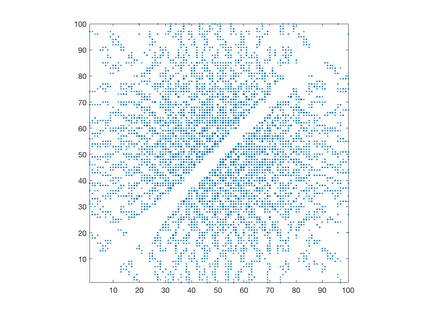
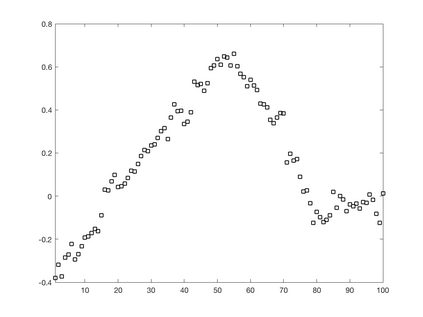
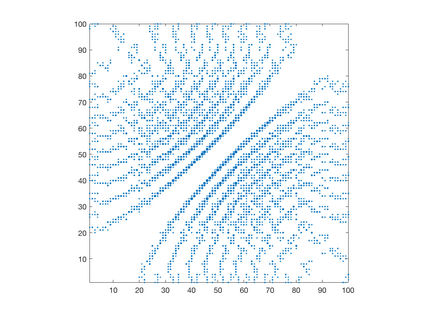
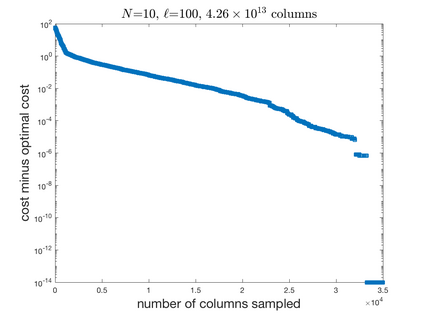
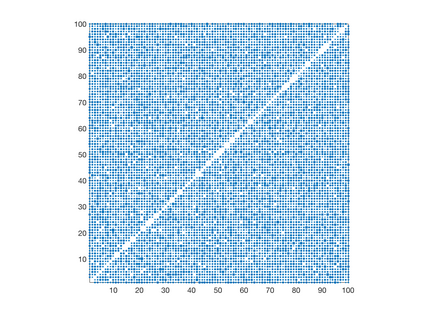
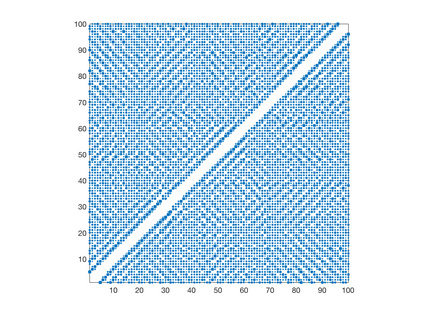
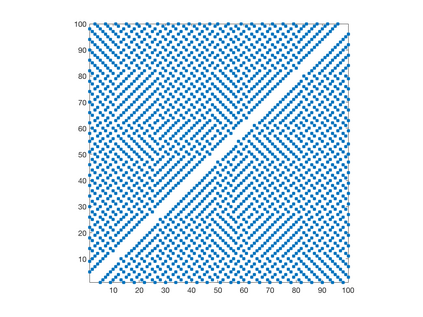
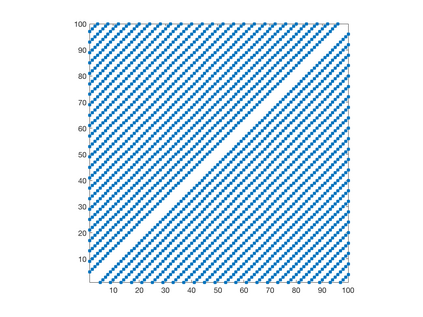
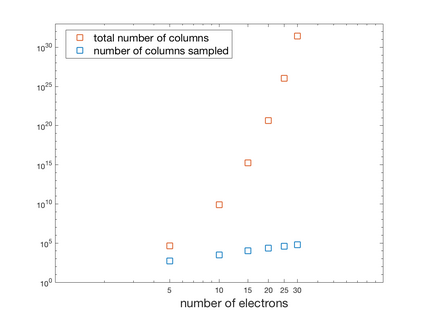
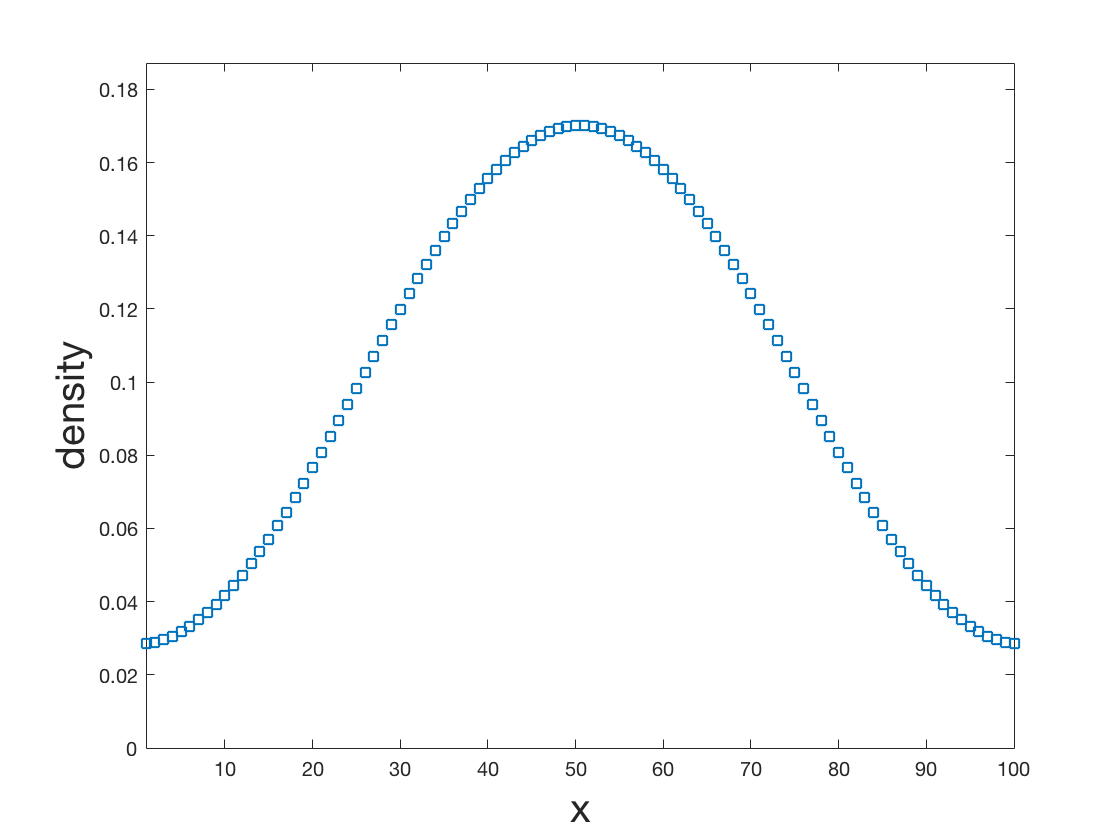
We introduce a simple, accurate, and extremely efficient method for numerically solving the multi-marginal optimal transport (MMOT) problems arising in density functional theory. The method relies on (i) the sparsity of optimal plans [for $N$ marginals discretized by $\ell$ gridpoints each, general Kantorovich plans require $\ell^N$ gridpoints but the support of optimizers is of size $O(\ell\cdot N)$ [FV18]], (ii) the method of column generation (CG) from discrete optimization which to our knowledge has not hitherto been used in MMOT, and (iii) ideas from machine learning. The well-known bottleneck in CG consists in generating new candidate columns efficiently; we prove that in our context, finding the best new column is an NP-complete problem. To overcome this bottleneck we use a genetic learning method tailormade for MMOT in which the dual state within CG plays the role of an "adversary", in loose similarity to Wasserstein GANs. On a sequence of benchmark problems with up to 120 gridpoints and up to 30 marginals, our method always found the exact optimizers. Moreover, empirically the number of computational steps needed to find them appears to scale only polynomially when both $N$ and $\ell$ are simultaneously increased (while keeping their ratio fixed to mimic a thermodynamic limit of the particle system).
翻译:我们引入了一种简单、准确和极为高效的方法来从数字上解决密度功能理论中产生的多边最佳运输(MMOT)问题。该方法依赖于(一) 最佳计划的宽度[对于每个网格点均以美元等于美元分网格点分离的美元边缘,一般的Kantorovich计划需要1美元=N美元网格点,但是优化剂的支持是大小O(ell\cdot N)$[FV18]]],(二) 从离散优化中生成(CG),但根据我们的知识在MMOT中一直没有使用,以及(三) 机器学习中的想法。CG中众所周知的瓶颈是高效生成新的候选列;我们证明在我们的背景下,找到最好的新列是一个NP-完整的问题。为了克服这一瓶颈,我们使用一种适合MMOT的遗传学习方法,使CGOT的双重状态起到“反向”的作用,与Wasserstein GANs有着不相近的相似的作用。在最边缘和最接近的顺序上,在最接近于最接近于最接近的30的计算方法时,在最接近于最接近于最接近于最接近于最接近的顺序的轨道的顺序的顺序上找到其最接近于最接近的30的轨道的轨道的顺序,直到最接近于最接近于最接近于最接近于最接近的计算方法。