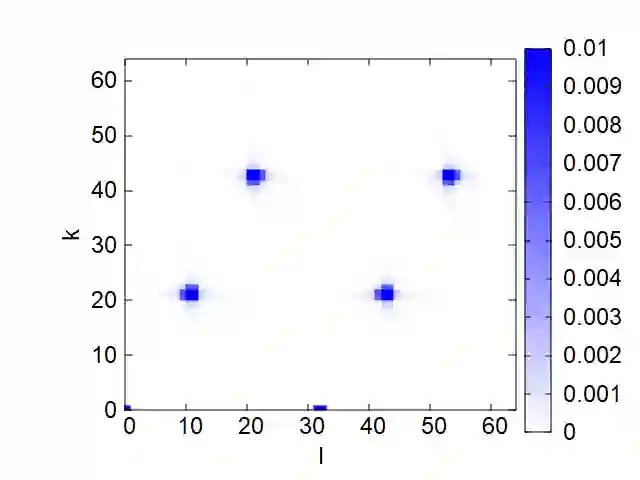
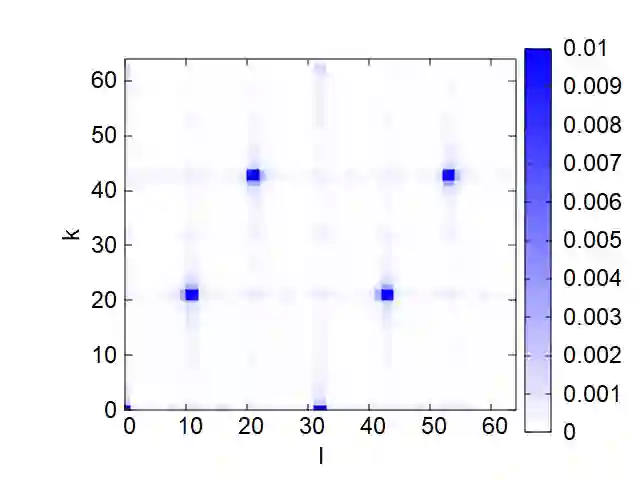
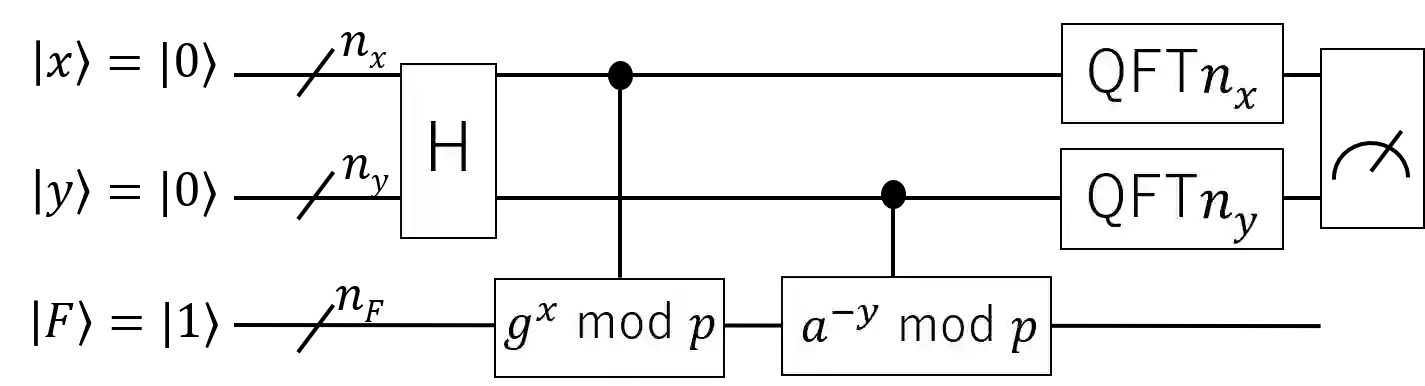The discrete logarithm problem (DLP) is the basis for several cryptographic primitives. Since Shor's work, it has been known that the DLP can be solved by combining a polynomial-size quantum circuit and a polynomial-time classical post-processing algorithm. Evaluating and predicting the instance size that quantum devices can solve is an emerging research topic. In this paper, we propose a quantitative measure based on the success probability of the post-processing algorithm to determine whether an experiment on a quantum device (or a classical simulator) succeeded. We also propose a procedure to modify bit strings observed from a Shor circuit to increase the success probability of a lattice-based post-processing algorithm. We report preliminary experiments conducted on IBM-Quantum quantum computers and near-future predictions based on noisy-device simulations. We conducted our experiments with the ibm_kawasaki device and discovered that the simplest circuit (7 qubits) from a 2-bit DLP instance achieves a sufficiently high success probability to proclaim the experiment successful. Experiments on another circuit from a slightly harder 2-bit DLP instance, on the other hand, did not succeed, and we determined that reducing the noise level by half is required to achieve a successful experiment. Finally, we give a near-term prediction based on required noise levels to solve some selected small DLP and integer factoring instances.
翻译:离散对数问题( DLP) 是数种加密原始数据的基础 。 自 Shor 的工作以来, 人们已经知道 DLP 可以通过将一个多米大小的量子电路和一个多米时间的经典后处理算法结合起来来解决。 评估和预测量子设备能够解决的体积是一个新出现的研究课题。 在本文中, 我们根据后处理算法的成功概率提出一个量化测量方法, 以确定量子设备( 或古典模拟器) 的实验是否成功。 我们还提议了一个程序, 修改从Shor 电路观测到的点字符串字符串, 以增加基于拉蒂的后处理算法的成功概率。 我们报告在IBM- 量子计算机上进行的初步实验, 以及根据噪声器模拟进行近距离预测。 我们用 ibm_ kawasaki 设备进行了实验, 并发现, 2比 DL 平方的简单电路程( 7 qubits) 使得一个足够的成功概率, 来宣布接近于 的 Drill 的实验成功率。 在另一个电路段级别上进行了略的实验, 需要 更难 。