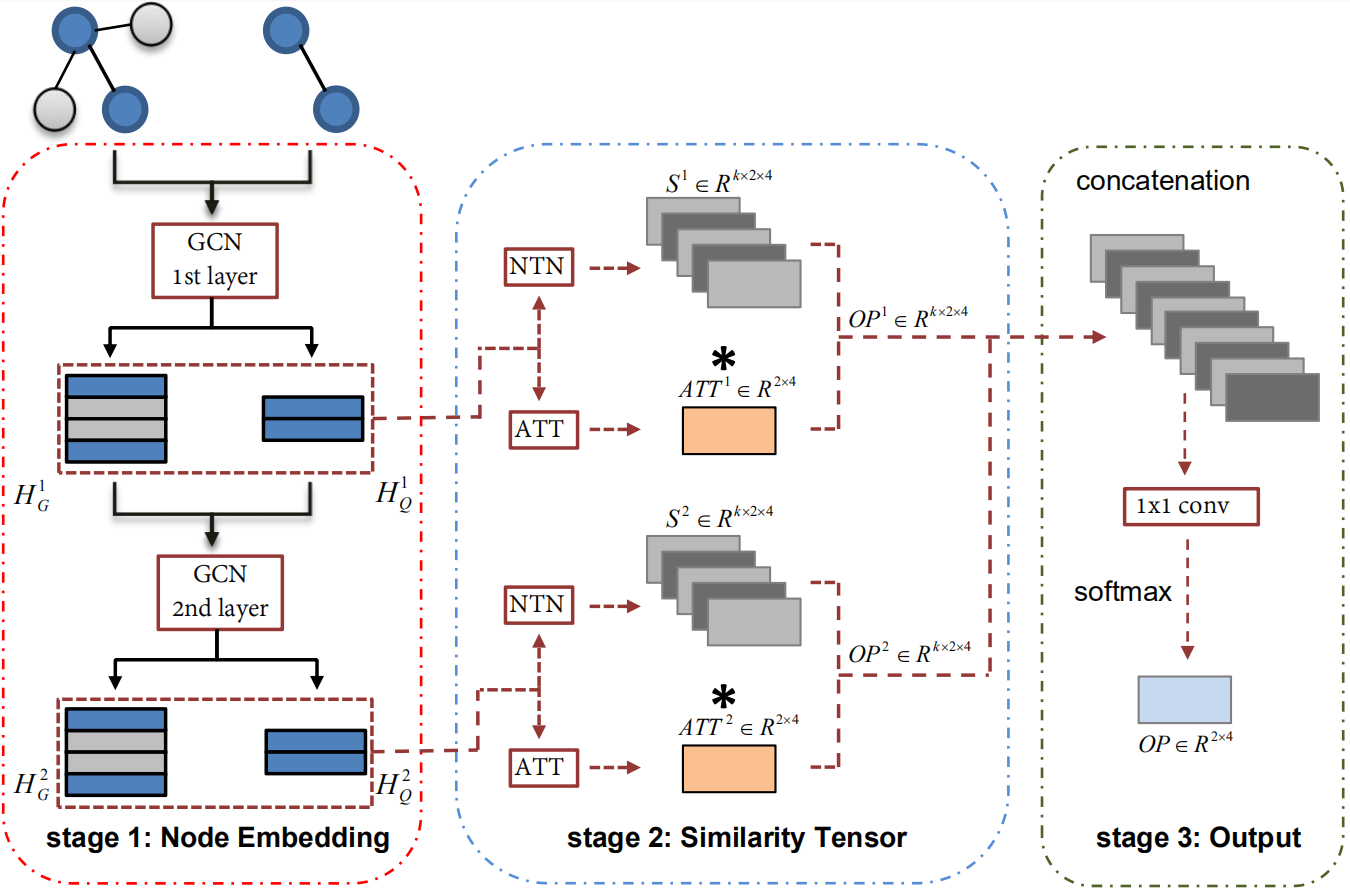
As one of the most fundamental tasks in graph theory, subgraph matching is a crucial task in many fields, ranging from information retrieval, computer vision, biology, chemistry and natural language processing. Yet subgraph matching problem remains to be an NP-complete problem. This study proposes an end-to-end learning-based approximate method for subgraph matching task, called subgraph matching network (Sub-GMN). The proposed Sub-GMN firstly uses graph representation learning to map nodes to node-level embedding. It then combines metric learning and attention mechanisms to model the relationship between matched nodes in the data graph and query graph. To test the performance of the proposed method, we applied our method on two databases. We used two existing methods, GNN and FGNN as baseline for comparison. Our experiment shows that, on dataset 1, on average the accuracy of Sub-GMN are 12.21\% and 3.2\% higher than that of GNN and FGNN respectively. On average running time Sub-GMN runs 20-40 times faster than FGNN. In addition, the average F1-score of Sub-GMN on all experiments with dataset 2 reached 0.95, which demonstrates that Sub-GMN outputs more correct node-to-node matches. Comparing with the previous GNNs-based methods for subgraph matching task, our proposed Sub-GMN allows varying query and data graphes in the test/application stage, while most previous GNNs-based methods can only find a matched subgraph in the data graph during the test/application for the same query graph used in the training stage. Another advantage of our proposed Sub-GMN is that it can output a list of node-to-node matches, while most existing end-to-end GNNs based methods cannot provide the matched node pairs.
翻译:作为图形理论中最基本的任务之一,子图匹配是许多领域的关键任务之一,包括信息检索、计算机视觉、生物学、化学和自然语言处理。但子图匹配问题仍然是NP不完整的问题。本研究为子图匹配任务提出了一个基于端到端学习的近似方法,称为子图匹配网络(Sub-GMN) 。拟议的子GMN首先使用图形代表学习来绘制节点到节点嵌入。然后,它将衡量学习和关注机制结合到模拟数据图表和查询图中匹配节点之间的关系。为了测试拟议方法的性能,我们在两个数据库中应用了我们的方法。我们使用两种现有方法,即GNNN和FGNNN作为子匹配的近似方法。在数据设置 1 上,子图匹配网络匹配网络的精度比GMN和FGNNN分别要高12.21和3.2英寸。在运行平均时间中,基于数据运行的子网/40倍,在数据测试过程中,用于所有实验阶段的子GNGN级测试中,在最高级的直径测试阶段平均F1和最高级的直径匹配数据中,在匹配的直径测试中,在前GND任务中,用于前的直径测试中,无法校对调数据中,在前的直调数据中,在匹配的轨道上调数据列表中,在匹配的直径程中,在匹配的直径程列表数据列表中,在运行中,在运行中,可以使数据列表中,在前的直径对调数据列表中,在比。