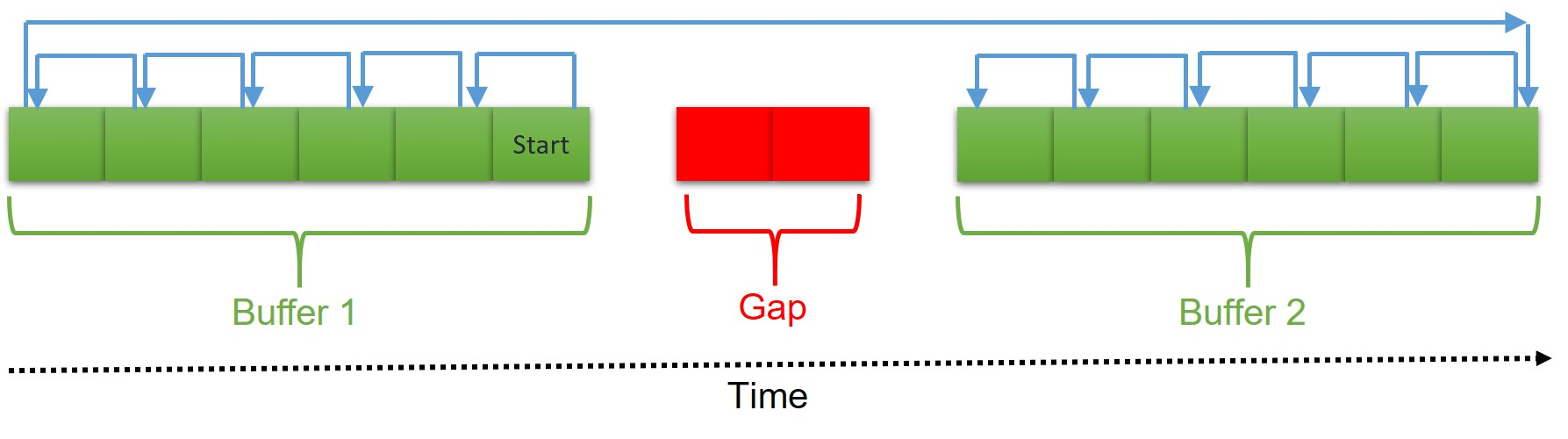
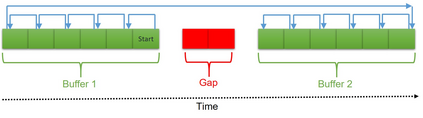
We consider the setting of vector valued non-linear dynamical systems $X_{t+1} = \phi(A^* X_t) + \eta_t$, where $\eta_t$ is unbiased noise and $\phi : \mathbb{R} \to \mathbb{R}$ is a known link function that satisfies certain {\em expansivity property}. The goal is to learn $A^*$ from a single trajectory $X_1,\cdots,X_T$ of {\em dependent or correlated} samples. While the problem is well-studied in the linear case, where $\phi$ is identity, with optimal error rates even for non-mixing systems, existing results in the non-linear case hold only for mixing systems. In this work, we improve existing results for learning nonlinear systems in a number of ways: a) we provide the first offline algorithm that can learn non-linear dynamical systems without the mixing assumption, b) we significantly improve upon the sample complexity of existing results for mixing systems, c) in the much harder one-pass, streaming setting we study a SGD with Reverse Experience Replay ($\mathsf{SGD-RER}$) method, and demonstrate that for mixing systems, it achieves the same sample complexity as our offline algorithm, d) we justify the expansivity assumption by showing that for the popular ReLU link function -- a non-expansive but easy to learn link function with i.i.d. samples -- any method would require exponentially many samples (with respect to dimension of $X_t$) from the dynamical system. We validate our results via. simulations and demonstrate that a naive application of SGD can be highly sub-optimal. Indeed, our work demonstrates that for correlated data, specialized methods designed for the dependency structure in data can significantly outperform standard SGD based methods.
翻译:我们认为设定矢量值的非线性动态系统 $X+1} =\phi(A ⁇ X_t) +\eta_t$ +\eta_t$, $\eta_t$是公正的噪音, $phi:\mathbb{R}\to\mathbb{R} 到\mathbb{R} 美元是一个已知的链接功能, 满足某些 {em 扩展属性} 。 目标是从单一轨道 $X_ 1,\cdots, X_T$ =美元, =美元依赖或关联} 样本 =\phi(A_xxxxx) +\\\\ a\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\