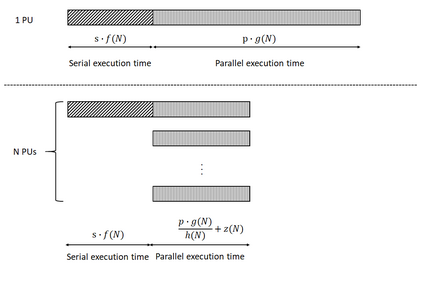
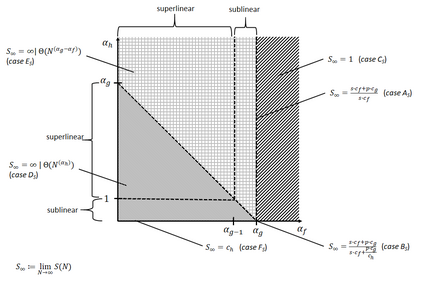
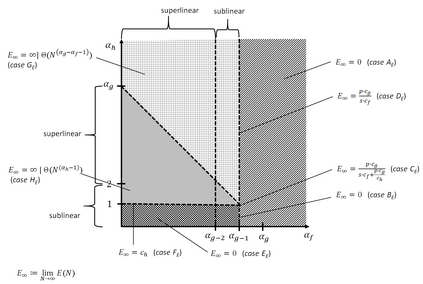
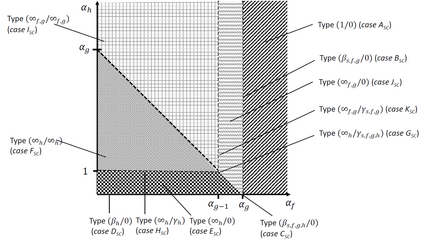
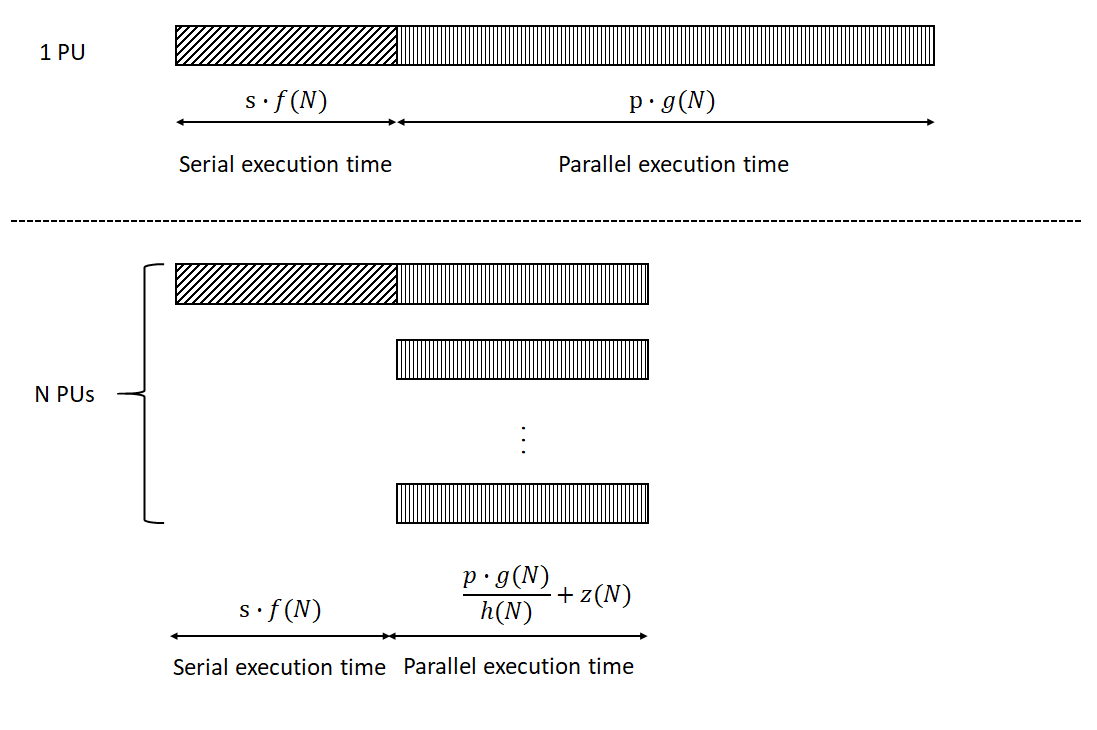
In high performance computing environments, we observe an ongoing increase in the available numbers of cores. This development calls for re-emphasizing performance (scalability) analysis and speedup laws as suggested in the literature (e.g., Amdahl's law and Gustafson's law), with a focus on asymptotic performance. Understanding speedup and efficiency issues of algorithmic parallelism is useful for several purposes, including the optimization of system operations, temporal predictions on the execution of a program, and the analysis of asymptotic properties and the determination of speedup bounds. However, the literature is fragmented and shows a large diversity and heterogeneity of speedup models and laws. These phenomena make it challenging to obtain an overview of the models and their relationships, to identify the determinants of performance in a given algorithmic and computational context, and, finally, to determine the applicability of performance models and laws to a particular parallel computing setting. In this work, we provide a generic speedup (and thus also efficiency) model for homogeneous computing environments. Our approach generalizes many prominent models suggested in the literature and allows showing that they can be considered special cases of a unifying approach. The genericity of the unifying speedup model is achieved through parameterization. Considering combinations of parameter ranges, we identify six different asymptotic speedup cases and eight different asymptotic efficiency cases. Jointly applying these speedup and efficiency cases, we derive eleven scalability cases, from which we build a scalability typology. Researchers can draw upon our typology to classify their speedup model and to determine the asymptotic behavior when the number of parallel processing units increases. In addition, our results may be used to address various extensions of our setting.
翻译:在高性能计算环境中,我们观察到现有核心数量持续增加。这一发展要求重新强调文学(例如Amdahl的法律和Gustafson的法律)所建议的业绩(可缩放性)分析和加速法,重点是无症状性表现。理解快速化和效率的算法平行问题对若干目的有用,包括优化系统操作、对程序执行的时间预测、对无症状特性的分析以及加速界限的确定。然而,文献是零散的,显示出加速模型和法律的高度多样性和不同性格。这些现象使得很难获得模型及其关系的概览,确定特定算法和计算环境中的业绩决定因素,以及最后,确定业绩模型和法律对特定平行计算设置的适用性。在这项工作中,我们可以为同质计算环境提供一个通用的加速(也因此也是效率)模型。我们的方法将许多突出的货币模型从加速性模型和加速性差异性化模型和加速性格模型的加速性和异性。这些现象使我们在采用通用性变异性研究案例时,可以确定我们不同性模型和变异性研究案例的精确性结果。我们用这些模型和变异性研究案例来确定我们所实现的合并。