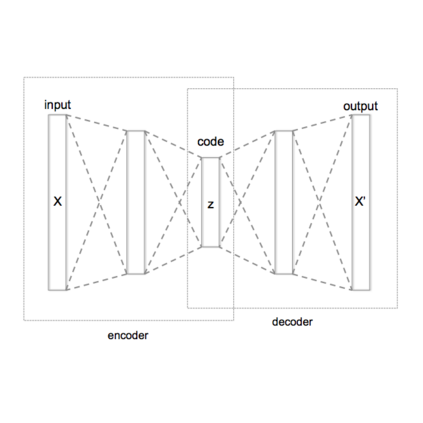
Variational Autoencoders (VAEs) and other generative models are widely employed in artificial intelligence to synthesize new data. However, current approaches rely on Euclidean geometric assumptions and statistical approximations that fail to capture the structured and emergent nature of data generation. This paper introduces the Convergent Fusion Paradigm (CFP) theory, a novel geometric framework that redefines data generation by integrating dimensional expansion accompanied by qualitative transformation. By modifying the latent space geometry to interact with emergent high-dimensional structures, CFP theory addresses key challenges such as identifiability issues and unintended artifacts like hallucinations in Large Language Models (LLMs). CFP theory is based on two key conceptual hypotheses that redefine how generative models structure relationships between data and algorithms. Through the lens of CFP theory, we critically examine existing metric-learning approaches. CFP theory advances this perspective by introducing time-reversed metric embeddings and structural convergence mechanisms, leading to a novel geometric approach that better accounts for data generation as a structured epistemic process. Beyond its computational implications, CFP theory provides philosophical insights into the ontological underpinnings of data generation. By offering a systematic framework for high-dimensional learning dynamics, CFP theory contributes to establishing a theoretical foundation for understanding the data-relationship structures in AI. Finally, future research in CFP theory will be led to its implications for fully realizing qualitative transformations, introducing the potential of Hilbert space in generative modeling.
翻译:暂无翻译