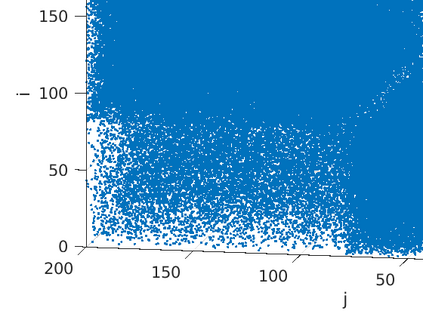
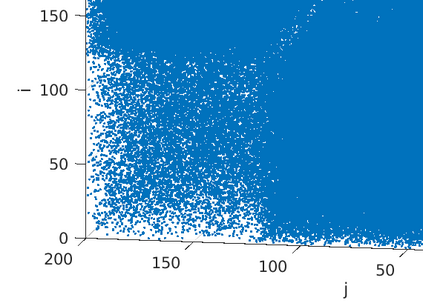
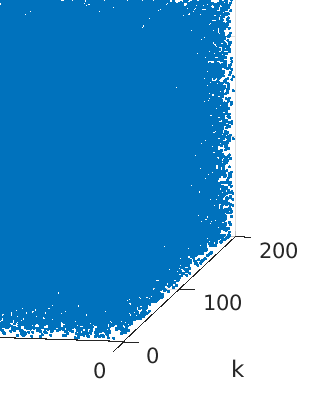
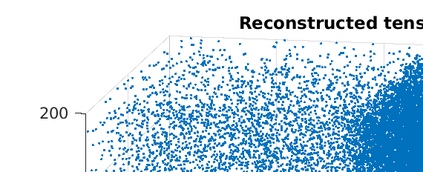
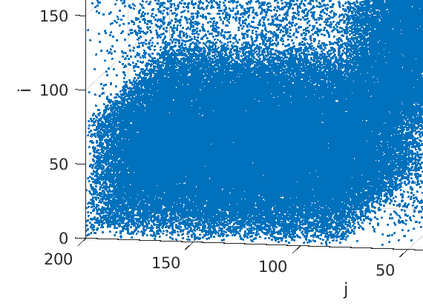
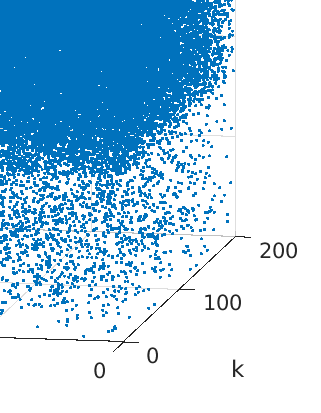
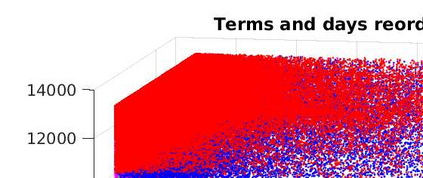
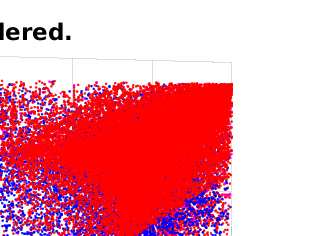
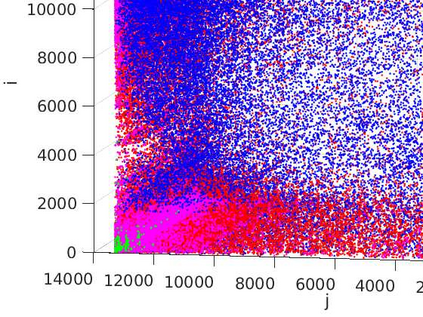
The problem of partitioning a large and sparse tensor is considered, where the tensor consists of a sequence of adjacency matrices. Theory is developed that is a generalization of spectral graph partitioning. A best rank-$(2,2,\lambda)$ approximation is computed for $\lambda=1,2,3$, and the partitioning is computed from the orthogonal matrices and the core tensor of the approximation. It is shown that if the tensor has a certain reducibility structure, then the solution of the best approximation problem exhibits the reducibility structure of the tensor. Further, if the tensor is close to being reducible, then still the solution of the exhibits the structure of the tensor. Numerical examples with synthetic data corroborate the theoretical results. Experiments with tensors from applications show that the method can be used to extract relevant information from large, sparse, and noisy data.
翻译:分解一个大而稀疏的沙粒的问题被考虑, 其压力是由一系列相邻基质组成。 理论的形成是光谱图分割的概括化。 最高等级( 2,\\ lambda) $= 1, 2, 3美元 的近似值计算为 $\ lambda= 1, 2, 3 美元, 分解是从正弦基质和近似核心分解的问题计算出来的。 事实证明, 如果粒子具有某种可复制性结构, 那么最佳近似问题的解决方案将展示出高压的可复制性结构。 此外, 如果粒子接近可再现, 则仍然能解决展出高压体的结构。 合成数据的数值例子将证实理论结果。 应用的强压实验显示, 可以用这种方法从大、 稀少和吵闹的数据中提取相关信息。