Geometric Embeddability of Complexes is $\exists \mathbb R$-complete

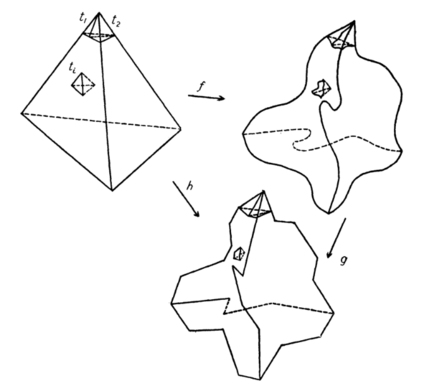
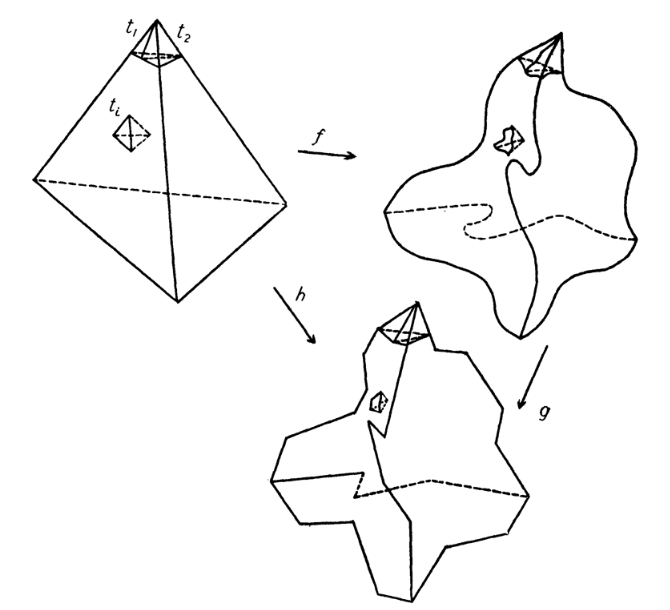
We show that the decision problem of determining whether a given (abstract simplicial) $k$-complex has a geometric embedding in $\mathbb R^d$ is complete for the Existential Theory of the Reals for all $d\geq 3$ and $k\in\{d-1,d\}$. This implies that the problem is polynomial time equivalent to determining whether a polynomial equation system has a real root. Moreover, this implies NP-hardness and constitutes the first hardness results for the algorithmic problem of geometric embedding (abstract simplicial) complexes.