On quadratic variations of the fractional-white wave equation

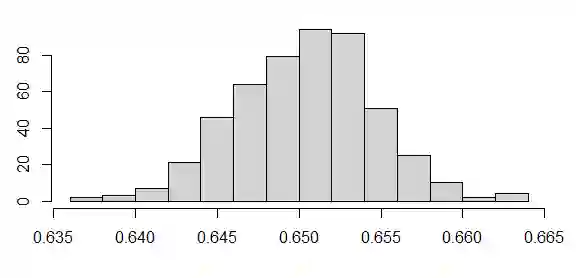
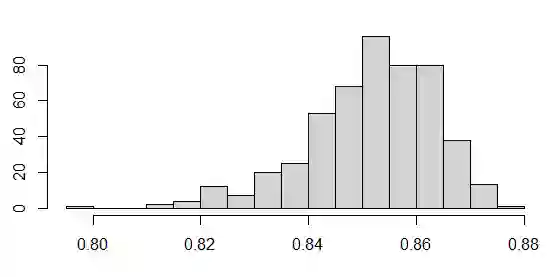
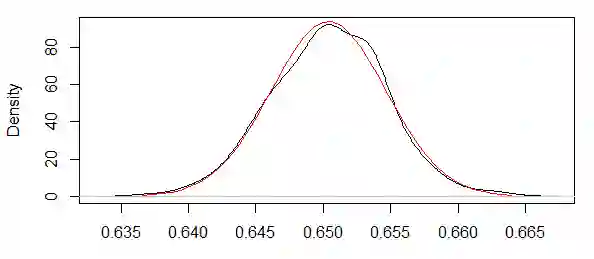
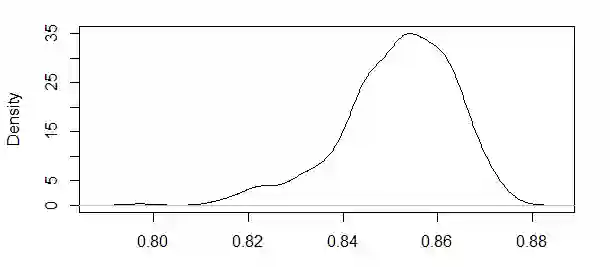
This paper studies the behaviour of quadratic variations of a stochastic wave equation driven by a noise that is white in space and fractional in time. Complementing the analysis of quadratic variations in the space component carried out by M. Khalil and C. A. Tudor (2018) and by R. Shevchenko, M. Slaoui and C. A. Tudor (2020), it focuses on the time component of the solution process. For different values of the Hurst parameter a central and a noncentral limit theorems are proved, allowing to construct consistent parameter estimators and compare them to the finding in the space-dependent case. Finally, rectangular quadratic variations in the white noise case are studied and a central limit theorem is demonstrated.