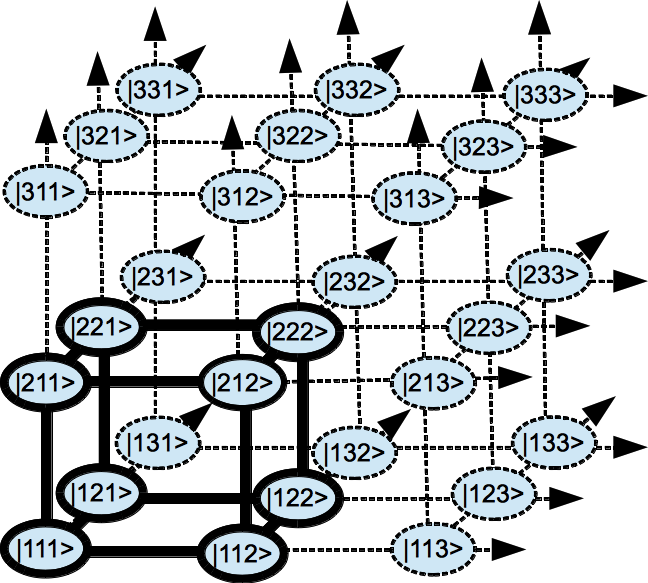
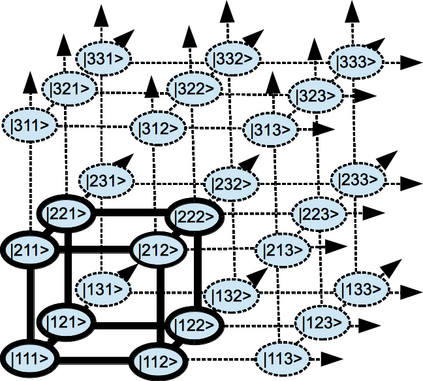
Informational dependence between statistical or quantum subsystems can be described with Fisher matrix or Fubini-Study metric obtained from variations of the sample/configuration space coordinates. Using these non-covariant objects as macroscopic constraints we consider statistical ensembles over the space of classical probability distributions or quantum wave-functions. The ensembles are covariantized using dual field theories with either complex or real scalar fields identified with complex wave-functions or square root of probabilities. We argue that a full space-time covariance on a field theory side is dual to local computations on the information theory side. We define a fully covariant information-computation tensor and show that it must satisfy conservation equations. Then we switch to a thermodynamic description and argue that the (inverse of) space-time metric tensor is a conjugate thermodynamic variable to the ensemble-averaged information-computation tensor. In the equilibrium the entropy production vanishes and the metric is not dynamical, but away from equilibrium the entropy production gives rise to an emergent dynamics of the metric. This dynamics can be described by expanding the entropy production into products of generalized forces (derivatives of metric) and conjugate fluxes. Near equilibrium these fluxes are given by an Onsager tensor contracted with generalized forces and on the grounds of time-reversal symmetry the Onsager tensor is expected to be symmetric. We show that a particularly simple and highly symmetric form of the Onsager tensor gives rise to the Einstein-Hilbert term. This proves that general relativity is equivalent to a theory of non-equilibrium (thermo)dynamics of the metric which is expected to break down far away from equilibrium where the symmetries of the Onsager tensor are to be broken.
翻译:统计或量子子子系统之间的信息依赖性可以用 Fisher 矩阵或 Fubini- study 度量来描述。 我们从样本/ 配置空间坐标的变异中获取的 Fisher 矩阵或 Fubini- Stududy 度量。 我们用这些非变量作为宏观限制来定义这些非变量物体。 我们认为, 在古典概率分布空间或量子波函数函数空间的统计集合。 组合使用复杂的或真实的波函数或概率平方根的双向地表理论来描述。 我们争辩说, 实地理论的完整时空共变异性是本地的计算的双重。 我们定义了完全变量信息- 空间变异性点, 信息理论方面的地方计算结果是双重的。 我们定义了完全变量信息变异异性数据, 显示它必须满足保护方等值。 然后我们换换换一个热力描述, 空间- 时间变异体将热性变异变异变异变异性变变异到 。 我们的变异性变异性生产和矩阵变异性变异性变异性变异性变异性变的变异性变异性变变变变变异性变异性变的变变异性变异性变异性变变变变变变变变, 。