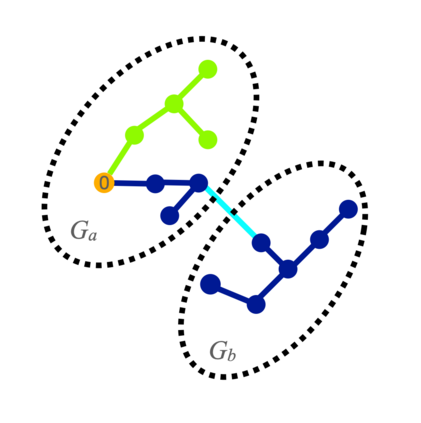
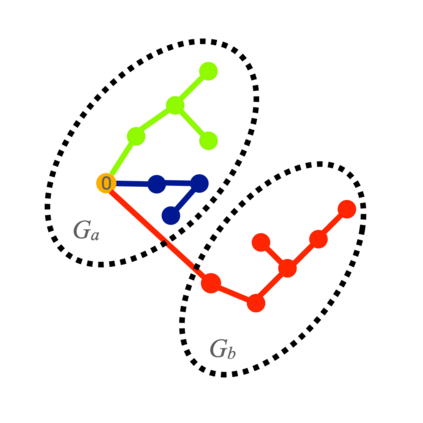
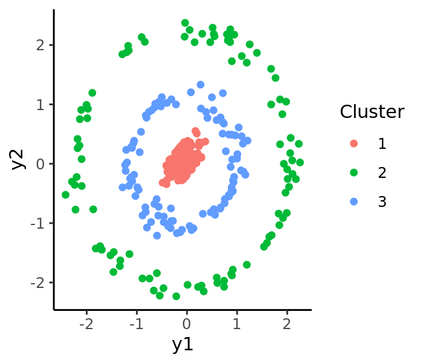
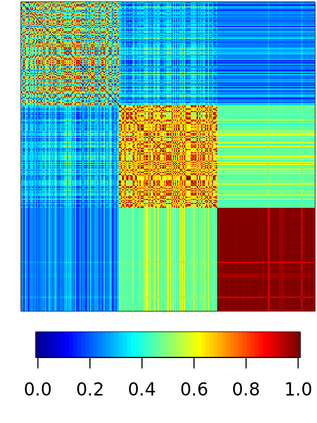
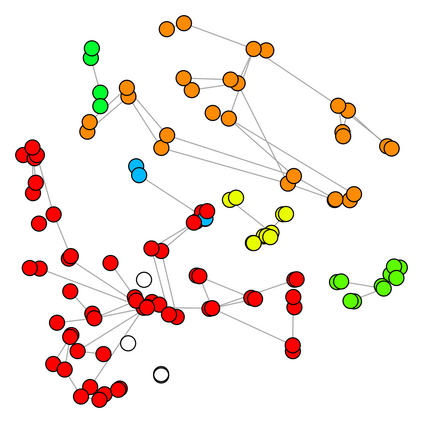
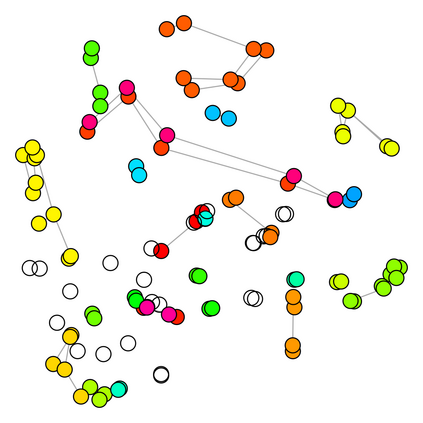
Spectral Clustering, Spanning Forest, and Bayesian Forest Process

Spectral clustering algorithms are very popular. Starting from a pairwise similarity matrix, spectral clustering gives a partition of data that approximately minimizes the total similarity scores across clusters. Since there is no need to model how data are distributed within each cluster, such a method enjoys algorithmic simplicity and robustness in clustering non-Gaussian data such as those near manifolds. Nevertheless, several important questions are unaddressed, such as how to estimate the similarity scores and cluster assignment probabilities, as important uncertainty estimates in clustering. In this article, we propose to solve these problems with a discovered generative modeling counterpart. Our clustering model is based on a spanning forest graph that consists of several disjoint spanning trees, with each tree corresponding to a cluster. Taking a Bayesian approach, we assign proper densities on the root and leaf nodes, and we prove that the posterior mode is almost the same as spectral clustering estimates. Further, we show that the associated generative process, named "forest process", is a continuous extension to the classic urn process, hence inheriting many nice properties such as having unbounded support for the number of clusters and being amenable to existing partition probability function; at the same time, we carefully characterize their differences. We demonstrate a novel application in joint clustering of multiple-subject functional magnetic resonance imaging scans of the human brain.