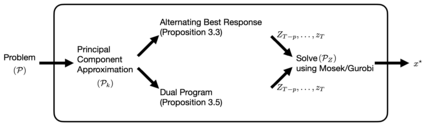
We propose a novel approximation hierarchy for cardinality-constrained, convex quadratic programs that exploits the rank-dominating eigenvectors of the quadratic matrix. Each level of approximation admits a min-max characterization whose objective function can be optimized over the binary variables analytically, while preserving convexity in the continuous variables. Exploiting this property, we propose two scalable optimization algorithms, coined as the "best response" and the "dual program", that can efficiently screen the potential indices of the nonzero elements of the original program. We show that the proposed methods are competitive with the existing screening methods in the current sparse regression literature, and it is particularly fast on instances with high number of measurements in experiments with both synthetic and real datasets.
翻译:我们为受限制的基点、 convex 二次方程式建议一个新的近似等级, 以利用四方矩阵中位居顶端的顶端成分。 每一级近似都承认一个微轴特征, 其客观功能可以通过分析优化于二进制变量, 同时保留连续变量的共性。 利用这一属性, 我们提出了两种可缩放的优化算法, 它们是“ 最佳响应” 和“双程序 ”, 可以有效筛选原程序非零元素的潜在指数。 我们显示, 所提议方法与当前微小回归文献中的现有筛选方法相比具有竞争力, 并且对于在合成和真实数据集实验中进行大量测量的事例来说, 尤其快速。