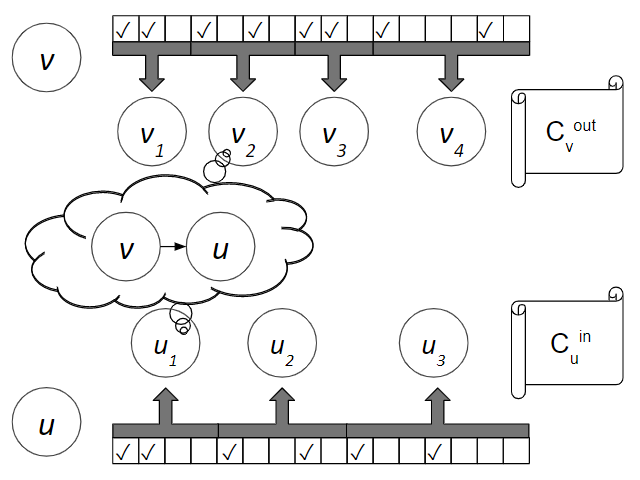
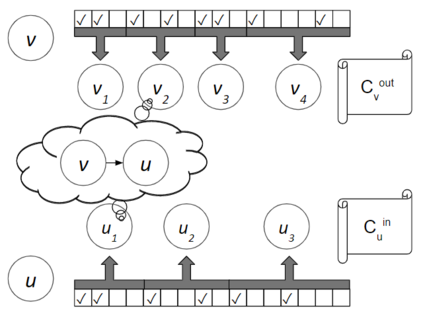
We extract a core principle underlying seemingly different fundamental distributed settings, showing sparsity awareness may induce faster algorithms for problems in these settings. To leverage this, we establish a new framework by developing an intermediate auxiliary model weak enough to be simulated in the CONGEST model given low mixing time, as well as in the recently introduced HYBRID model. We prove that despite imposing harsh restrictions, this artificial model allows balancing massive data transfers with high bandwidth utilization. We exemplify the power of our methods, by deriving shortest-paths algorithms improving upon the state-of-the-art. Specifically, we show the following for graphs of $n$ nodes: A $(3+\epsilon)$ approximation for weighted APSP in $(n/\delta)\tau_{mix}\cdot 2^{O(\sqrt\log n)}$ rounds in the CONGEST model, where $\delta$ is the minimum degree of the graph and $\tau_{mix}$ is its mixing time. For graphs with $\delta=\tau_{mix}\cdot 2^{\omega(\sqrt\log n)}$, this takes $o(n)$ rounds, despite the $\Omega(n)$ lower bound for general graphs [Nanongkai, STOC'14]. An $(n^{7/6}/m^{1/2}+n^2/m)\cdot\tau_{mix}\cdot 2^{O(\sqrt\log n)}$-round exact SSSP algorithm in the CONGNEST model, for graphs with $m$ edges and a mixing time of $\tau_{mix}$. This improves upon the algorithm of [Chechik and Mukhtar, PODC'20] for significant ranges of values of $m$ and $ \tau_{mix}$. A CONGESTED CLIQUE simulation in the CONGEST model improving upon the state-of-the-art simulation of [Ghaffari, Kuhn, and SU, PODC'17] by a factor proportional to the average degree in the graph. An $\tilde O(n^{5/17}/\epsilon^9)$-round algorithm for a $(1+\epsilon)$ approximation for SSSP in the HYBRID model. The only previous $o(n^{1/3})$ round algorithm for distance approximations in this model is for a much larger factor [Augustine, Hinnenthal, Kuhn, Scheideler, Schneider, SODA'20].
翻译:我们从表面上不同的基本分布设置中提取了一个核心原则, 显示磁度可能会在这些设置中引发更快的算法 。 为了利用这一点, 我们建立了一个新的框架。 我们开发了一个中间辅助模型, 在混合时间过低的情况下, 能够在 CONEST 模型中模拟 。 我们证明, 尽管施加了严格的限制, 这个人工模型可以平衡大量数据传输, 并且使用高带宽。 我们展示了我们方法的力量, 通过在最先进的模型中得出最短路径算法改进。 具体地说, 我们为 $的节点绘制了以下的图 : A( 3) QEepsielon, 在 CONESTEST 模型中模拟 $( sqrt\log n) 。 以普通的 美元计算, 以普通的 $( $) 平价计算, 以普通的 美元 平价计算, 以平价计算 和 美元平面的 。