A fast and simple modification of Newton's method helping to avoid saddle points

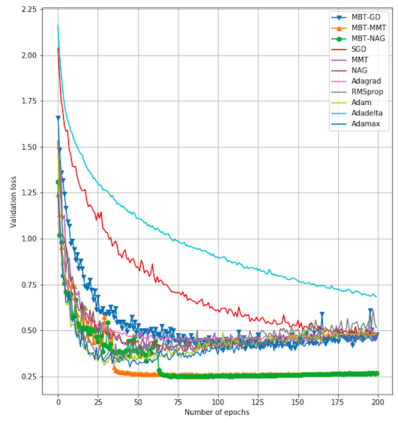
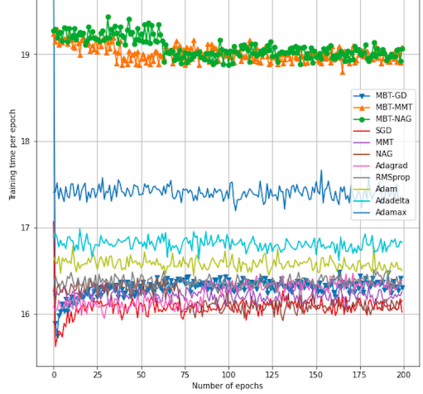
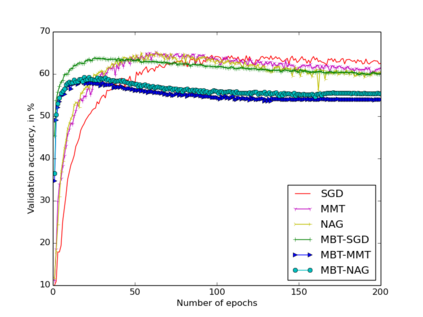
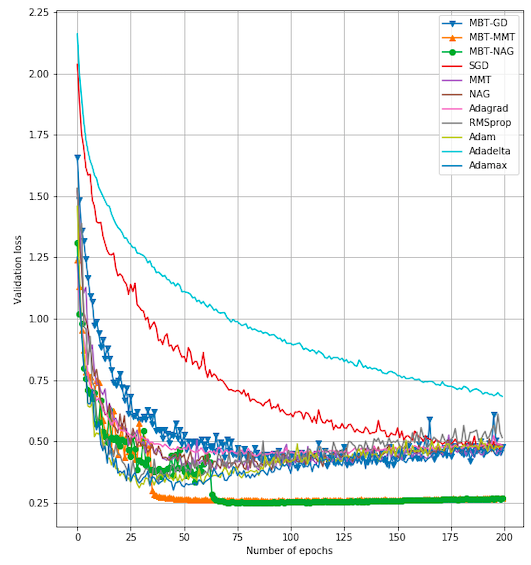
We propose in this paper New Q-Newton's method. The update rule for the simplest version is $x_{n+1}=x_n-w_n$ where $w_n=pr_{A_n,+}(v_n)-pr_{A_n,-}(v_n)$, with $A_n=\nabla ^2f(x_n)+\delta _n||\nabla f(x_n)||^2.Id$ and $v_n=A_n^{-1}.\nabla f(x_n)$. Here $\delta _n$ is an appropriate real number so that $A_n$ is invertible, and $pr_{A_n,\pm}$ are projections to the vector subspaces generated by eigenvectors of positive (correspondingly negative) eigenvalues of $A_n$. The main result of this paper roughly says that if $f$ is $C^3$ and a sequence $\{x_n\}$, constructed by the New Q-Newton's method from a random initial point $x_0$, {\bf converges}, then the limit point is a critical point and is not a saddle point, and the convergence rate is the same as that of Newton's method. At the end of the paper, we present some issues (saddle points and convergence) one faces when implementing Newton's method and modifications into Deep Neural Networks. In the appendix, we test the good performance of New Q-Newton's method on various benchmark test functions such as Rastrigin, Askley, Rosenbroch and many other, against algorithms such as Newton's method, BFGS, Adaptive Cubic Regularization, Random damping Newton's method and Inertial Newton's method, as well as Unbounded Two-way Backtracking Gradient Descent. The experiments demonstrate in particular that the assumption that $f$ is $C^3$ is necessary for some conclusions in the main theoretical results.