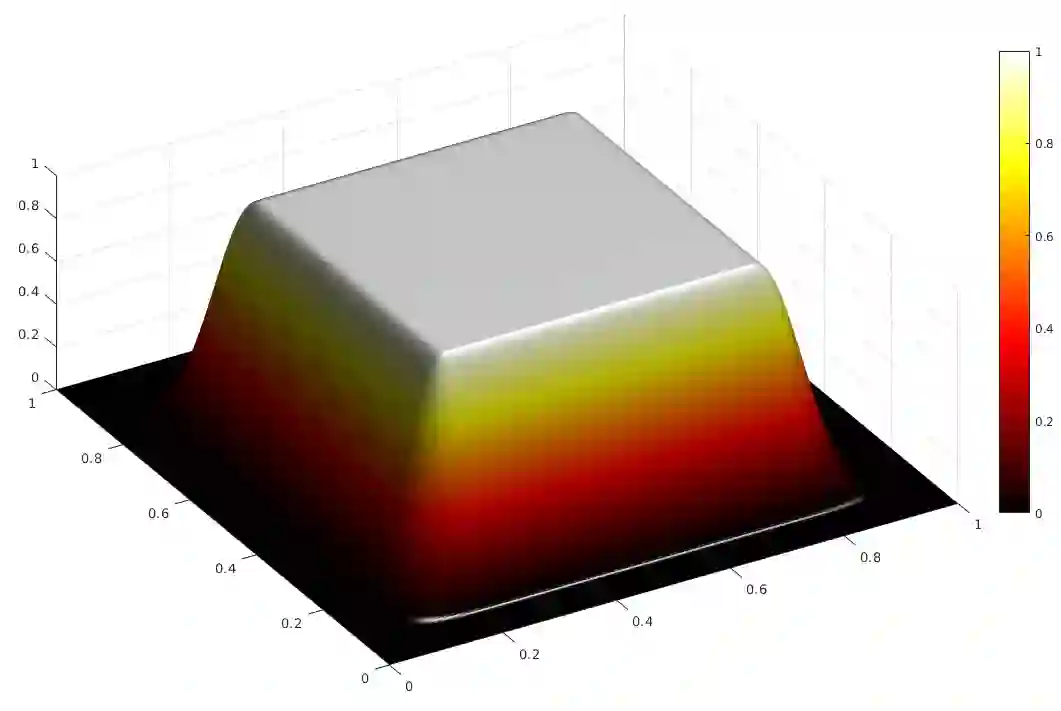
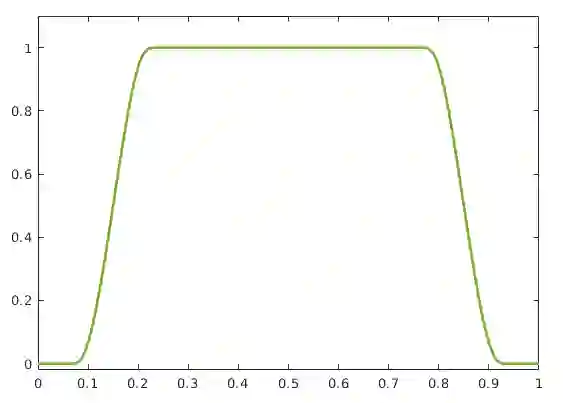
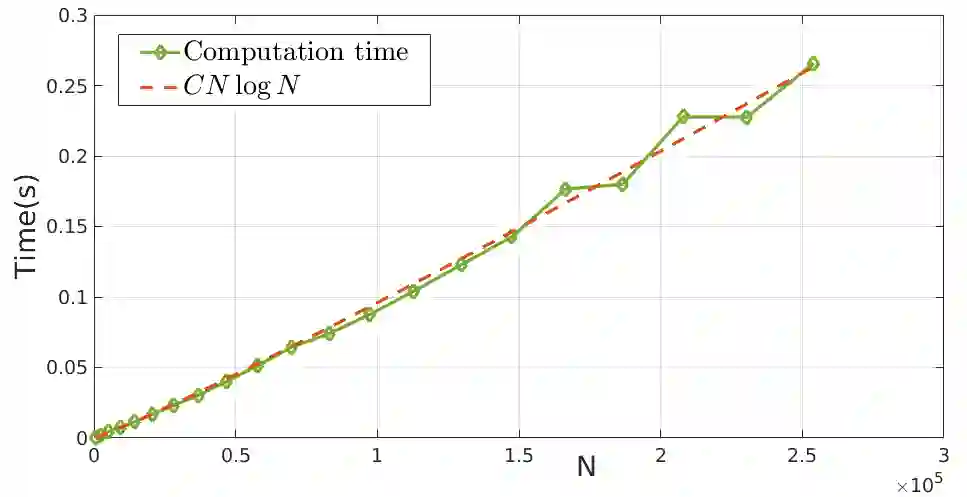
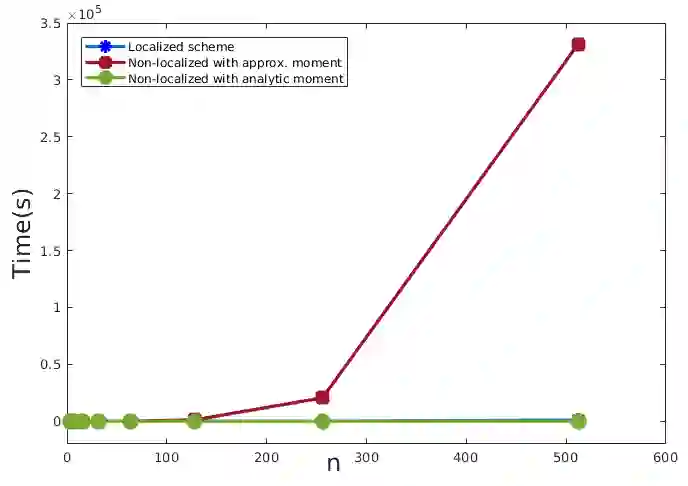
In this article, we present an $O(N \log N)$ rapidly convergent algorithm for the numerical approximation of the convolution integral with radially symmetric weakly singular kernels and compactly supported densities. To achieve the reduced computational complexity, we utilize the Fast Fourier Transform (FFT) on a uniform grid of size $N$ for approximating the convolution. To facilitate this and maintain the accuracy, we primarily rely on a periodic Fourier extension of the density with a suitably large period depending on the support of the density. The rate of convergence of the method increases with increasing smoothness of the periodic extension and, in fact, approximations exhibit super-algebraic convergence when the extension is infinitely differentiable. Furthermore, when the density has jump discontinuities, we utilize a certain Fourier smoothing technique to accelerate the convergence to achieve the quadratic rate in the overall approximation. Finally, we apply the integration scheme for numerical solution of certain partial differential equations. Moreover, we apply the quadrature to obtain a fast and high-order Nyst\"om solver for the solution of the Lippmann-Schwinger integral equation. We validate the performance of the proposed scheme in terms of accuracy as well as computational efficiency through a variety of numerical experiments.
翻译:在本篇文章中,我们展示了一种美元(N\log N)的快速趋同算法,用于分流集成与极微弱单单内核和精密支持的密度的对齐。为了实现较低的计算复杂性,我们将快速傅里叶变形(FFT)放在一个大小一致的网格上,以近似卷变形。为了便利这个过程并保持准确性,我们主要依靠一个定期的四面形扩大密度,视密度支持程度而定,有一个适当的大时期。方法的趋同速度随着周期扩展的日益平稳而加快,事实上,当延长的极小时,近似显示出超正轨趋同。此外,当密度突飞过不均时,我们使用某种四面形变变变变变变变法(FFT),以加速趋同速度在总体接近时达到四面形率。最后,我们运用了某种局部差方形方程式的数值解决方案。此外,我们运用四面形组合,以获得快速和高度的Nyst\”等同速度的趋同速度,在扩展时,在无限的延长的延长期中显示出超正值的加速的趋同性反应,作为通过Lippmann的计算法的计算方法,作为完整的计算方法的精确性平准的计算方法,作为Lippmann-creal-stalalgalgal-caldaldalpalpalpaldalgyaldaldalgyalgypalpal)的计算方法,作为一个完整的计算法的计算法的计算方法,作为一个完整的计算方法,作为一个完整的计算方法的精确的精确性平。
相关内容
- Today (iOS and OS X): widgets for the Today view of Notification Center
- Share (iOS and OS X): post content to web services or share content with others
- Actions (iOS and OS X): app extensions to view or manipulate inside another app
- Photo Editing (iOS): edit a photo or video in Apple's Photos app with extensions from a third-party apps
- Finder Sync (OS X): remote file storage in the Finder with support for Finder content annotation
- Storage Provider (iOS): an interface between files inside an app and other apps on a user's device
- Custom Keyboard (iOS): system-wide alternative keyboards
Source: iOS 8 Extensions: Apple’s Plan for a Powerful App Ecosystem