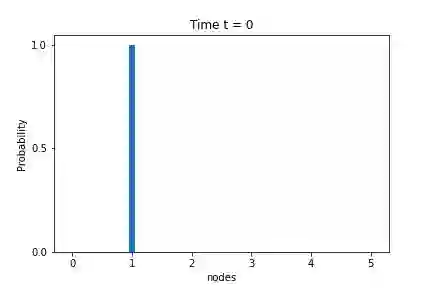
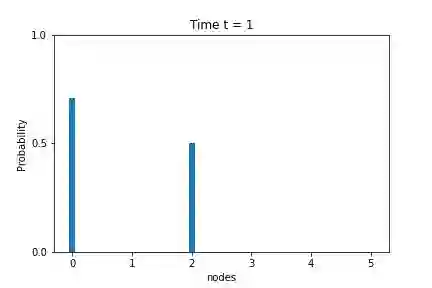
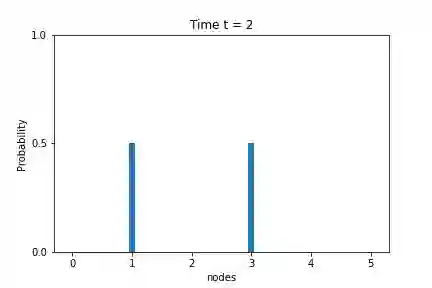
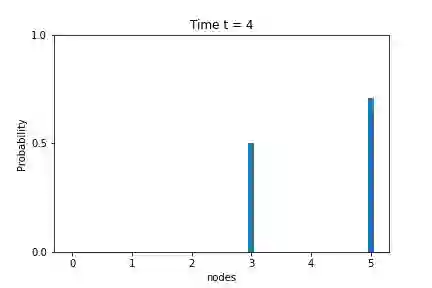
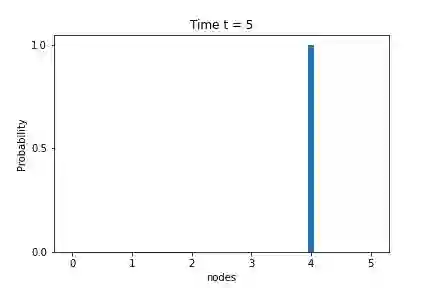
Quantum Perfect State Transfer (PST) is a fundamental tool of quantum communication in a network. It is considered a rare phenomenon. The original idea of PST depends on the fundamentals of the continuous-time quantum walk. A path graph with at most three vertices allows PST. Based on the Markovian quantum walk, we introduce a significantly powerful method for PST in this article. We establish PST between the extreme vertices of a path graph of arbitrary length. Moreover, any pair of vertices $j$ and $n - j - 1$ in a path graph with $n$ vertices allow PST for $0 \leq j < \frac{n - 1}{2}$. Also, no cycle graph with more than $4$ vertices does not allow PST based on the continuous-time quantum walk. In contrast, we establish PSTs based on Markovian quantum walk between the pair of vertices $j$ and $j + m$ for $j = 0, 1, \dots (m - 1)$ in a cycle graph with $2m$ vertices.
翻译:量子完美状态传输(PST) 是一个网络量子通信的基本工具。 它被认为是一种罕见的现象。 PST 的最初概念取决于连续时间量子漫步的基本原理。 一个最多有三个顶点的路径图允许 PST 。 基于 Markovian 量子漫步, 我们在此文章中引入了一个非常强大的 PST 方法 。 我们在一个任意长度路径图的极端顶点之间建立 PST 。 此外, 在一条路径图中, 任何两对顶点和 j - j - 1 美元, 以 $ $ 为零\ leq j < frac{n - 1 ⁇ 2} 允许 PST 基本原理。 另外, 4 美元以上顶点的循环图不允许 PST 以连续量漫步为基础 。 相反, 我们根据 4 j 美元 美元 和 美元 + 美元 美元 + m 美元以 $j= 0, 1 美元以 以 以 以 美元 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以 以