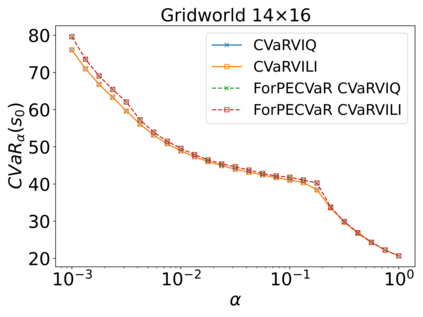
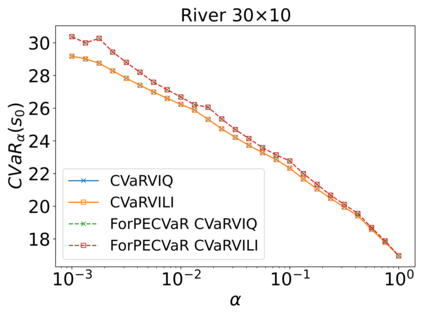
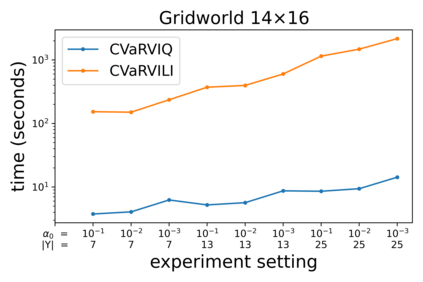
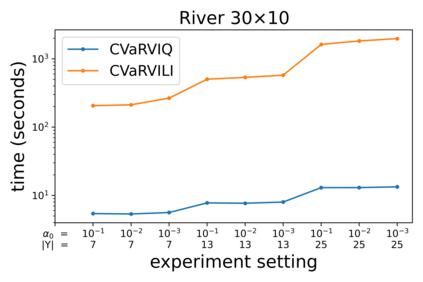
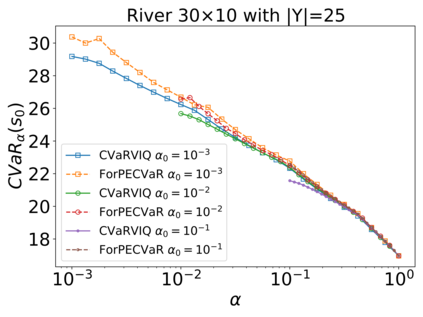
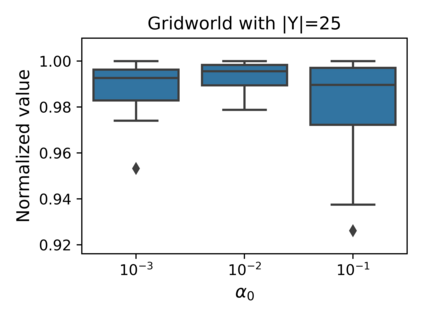
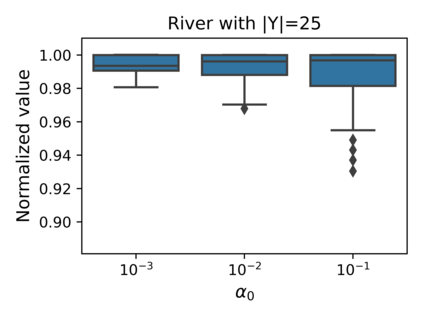
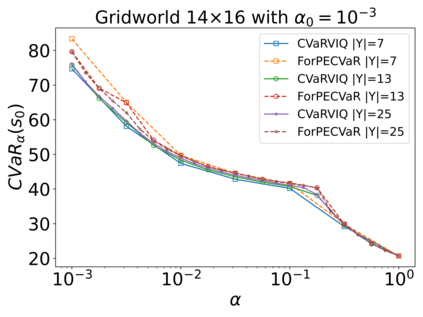
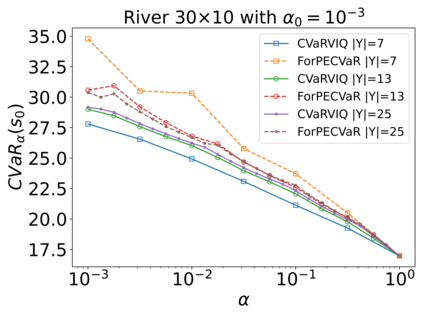
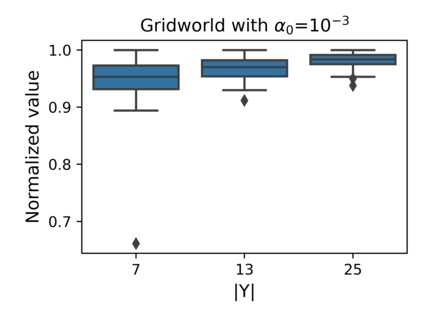
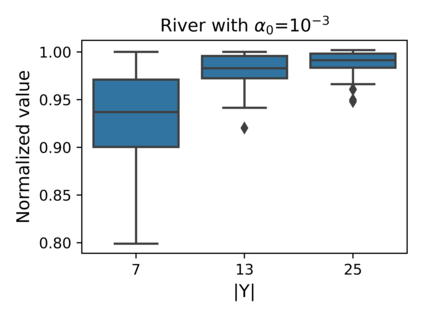
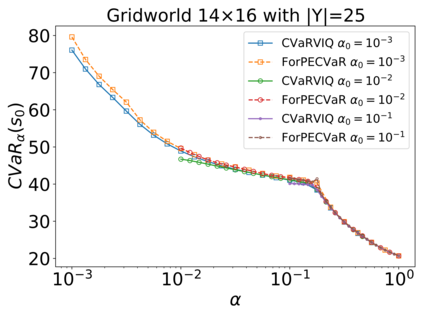
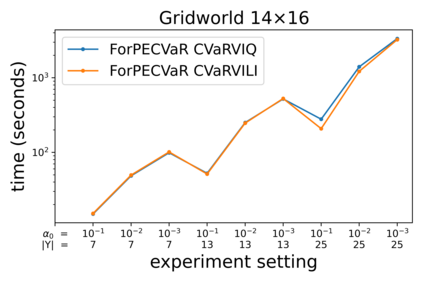
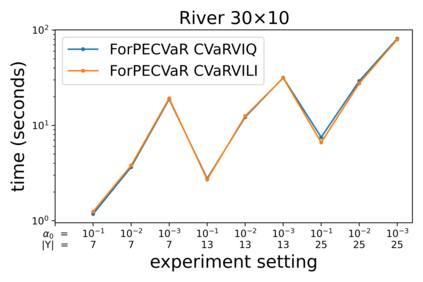
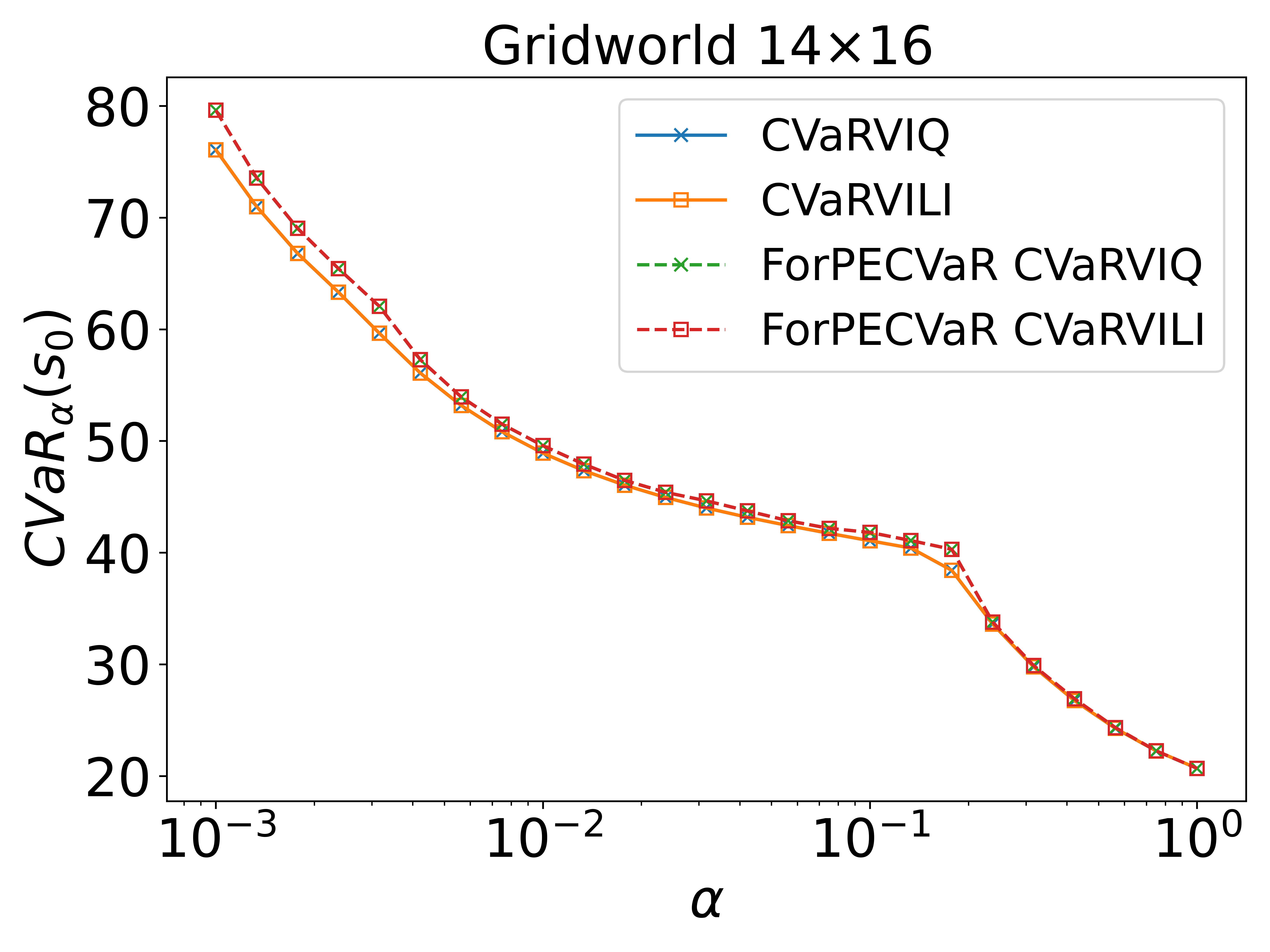
The Stochastic Shortest Path (SSP) problem models probabilistic sequential-decision problems where an agent must pursue a goal while minimizing a cost function. Because of the probabilistic dynamics, it is desired to have a cost function that considers risk. Conditional Value at Risk (CVaR) is a criterion that allows modeling an arbitrary level of risk by considering the expectation of a fraction $\alpha$ of worse trajectories. Although an optimal policy is non-Markovian, solutions of CVaR-SSP can be found approximately with Value Iteration based algorithms such as CVaR Value Iteration with Linear Interpolation (CVaRVIQ) and CVaR Value Iteration via Quantile Representation (CVaRVILI). These type of solutions depends on the algorithm's parameters such as the number of atoms and $\alpha_0$ (the minimum $\alpha$). To compare the policies returned by these algorithms, we need a way to exactly evaluate stationary policies of CVaR-SSPs. Although there is an algorithm that evaluates these policies, this only works on problems with uniform costs. In this paper, we propose a new algorithm, Forward-PECVaR (ForPECVaR), that evaluates exactly stationary policies of CVaR-SSPs with non-uniform costs. We evaluate empirically CVaR Value Iteration algorithms that found solutions approximately regarding their quality compared with the exact solution, and the influence of the algorithm parameters in the quality and scalability of the solutions. Experiments in two domains show that it is important to use an $\alpha_0$ smaller than the $\alpha$ target and an adequate number of atoms to obtain a good approximation.
翻译:斯托卡最短路径( SSP) 问题模型( SSP), 代理商必须在最小化成本功能的同时追求一个目标, 稳定连续决定问题。 由于概率动态, 它希望具有成本功能来考虑风险。 风险中条件值( CVaR) 是一个标准, 可以通过考虑微小的美元和美元等更差的轨迹来构建任意风险水平。 虽然最佳政策是非马可维值, 但CVAR- SSP的解决方案可以找到与价值透析法( 数值基值) 的算法相近的解决方案, 比如 CVAR 价值递升算法( CVRVIQ) 和 CVAR 值透算法( CVR- SSP 算法) 等基于价值透析法的算法( CVR- Slationalationalational 运算法( CVRR- Splationalationalation) 的算法( 值), 这些算法的参数只能用来比CVR- Sqlational 的算法( 运算法), 这些算法的算法是一个新的算法, 这些算法的比CForlation 成本政策更接近一个成本。</s>