Explicit numerical method for highly non-linear time-changed stochastic differential equations

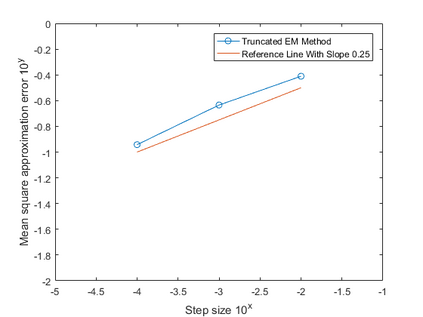
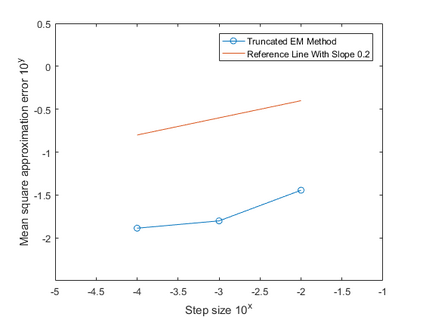
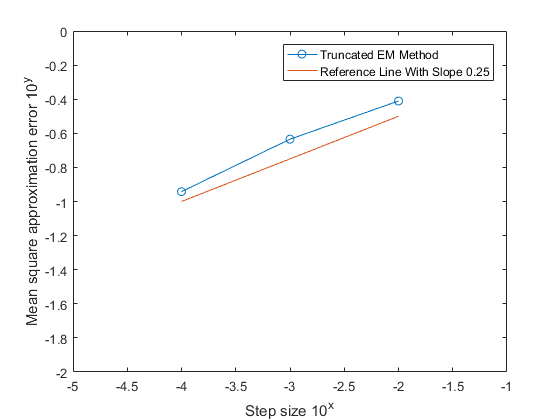
An explicit numerical method is developed for a class of time-changed stochastic differential equations, whose the coefficients obey H\"older's continuity in terms of the time variable and are allowed to grow super-linearly in terms of the state variable. The strong convergence of the method in a finite time interval is proved and the convergence rate is obtained. Numerical simulations are provided, which are in line with those theoretical results.