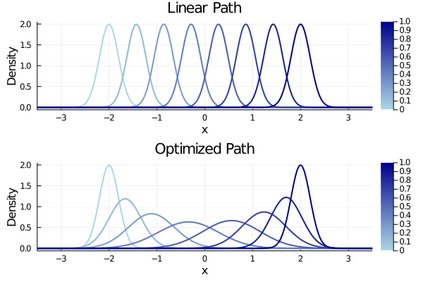
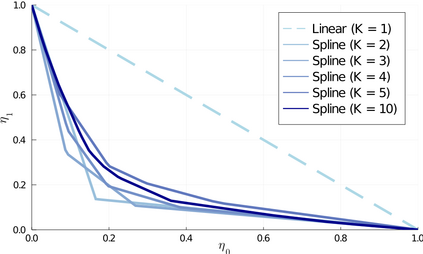
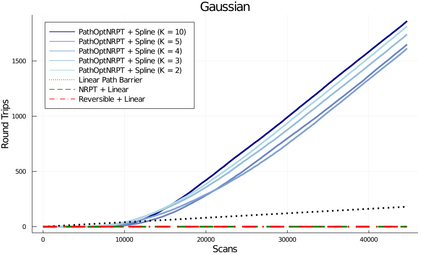
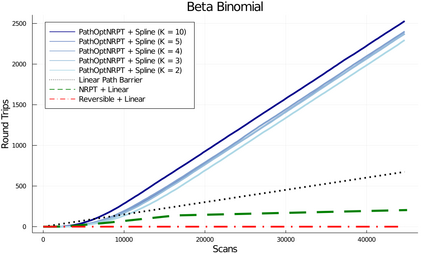
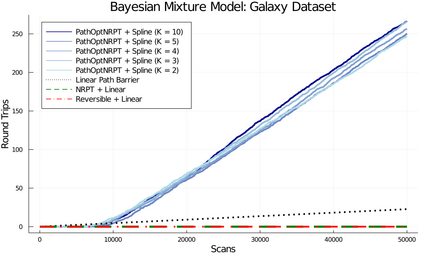
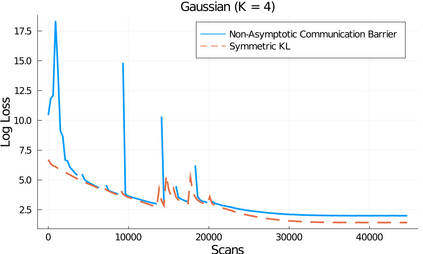
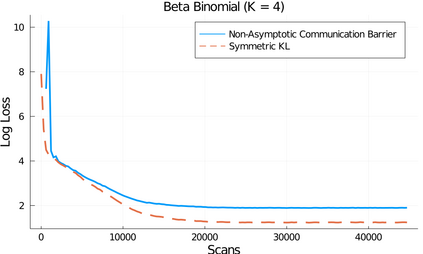
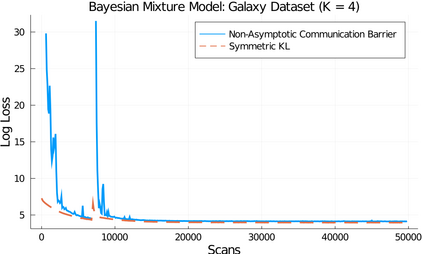
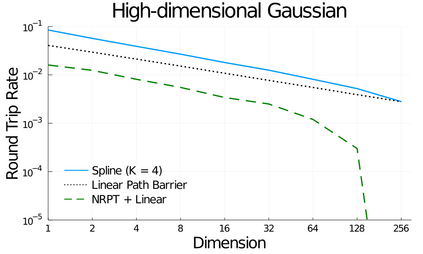
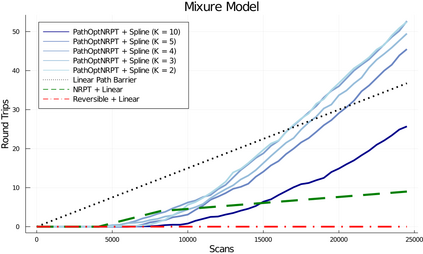
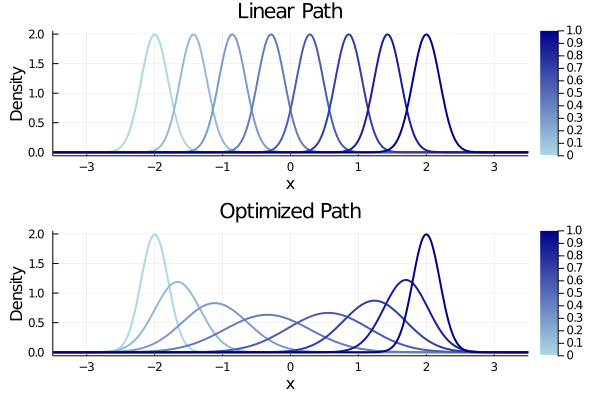
Parallel tempering (PT) is a class of Markov chain Monte Carlo algorithms that constructs a path of distributions annealing between a tractable reference and an intractable target, and then interchanges states along the path to improve mixing in the target. The performance of PT depends on how quickly a sample from the reference distribution makes its way to the target, which in turn depends on the particular path of annealing distributions. However, past work on PT has used only simple paths constructed from convex combinations of the reference and target log-densities. This paper begins by demonstrating that this path performs poorly in the setting where the reference and target are nearly mutually singular. To address this issue, we expand the framework of PT to general families of paths, formulate the choice of path as an optimization problem that admits tractable gradient estimates, and propose a flexible new family of spline interpolation paths for use in practice. Theoretical and empirical results both demonstrate that our proposed methodology breaks previously-established upper performance limits for traditional paths.
翻译:平行色调( PT) 是马可夫连锁 Monte Carlo 算法的一类, 它在可移植引用和目标之间构建了一条分布路径, 在可移植引用和棘手的目标之间形成一条透射路径, 然后交换会指出改善目标中混合的路径。 PT 的性能取决于引用分布的样本到目标的速度, 而这反过来又取决于肛交分布的特定路径。 但是, 过去关于 PT 的工作只使用了从引用和目标日志密度的曲线组合中构建的简单路径。 本文首先展示了这条路径在参考和目标几乎相互一致的设置中表现不佳。 为了解决这个问题, 我们把 PT 框架扩展至路径的普通组别, 将路径的选择设计成一个允许可移动梯度估计的优化问题, 并提出一个灵活的新链条内插图, 供实践使用。 理论和实证结果都表明, 我们拟议的方法打破了传统路径先前设定的高级性能限制 。