The Power of Alignment-Free Histogram-based Functions: a Comprehensive Genome Scale Experimental Analysis -- Version 2

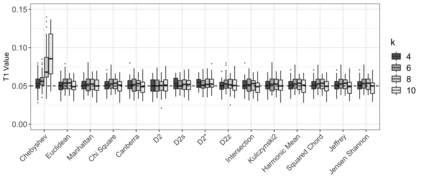
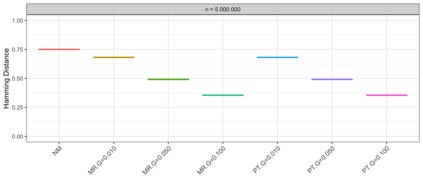
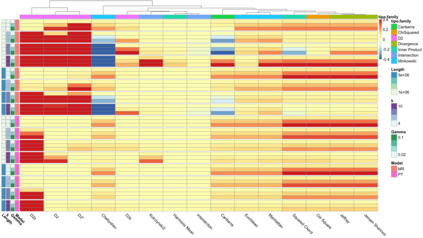
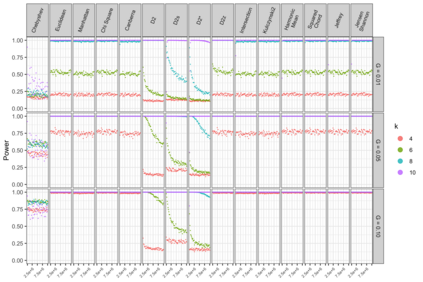
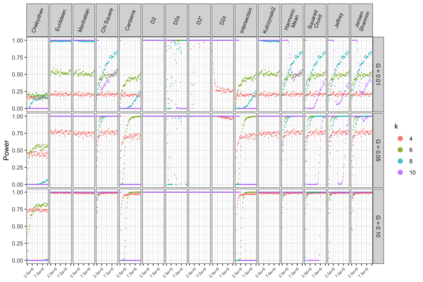
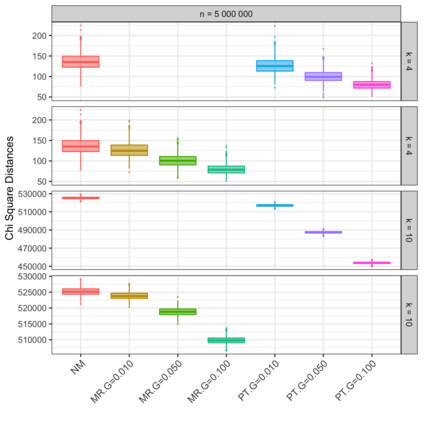
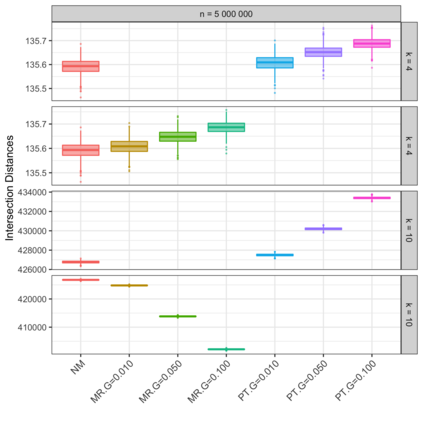
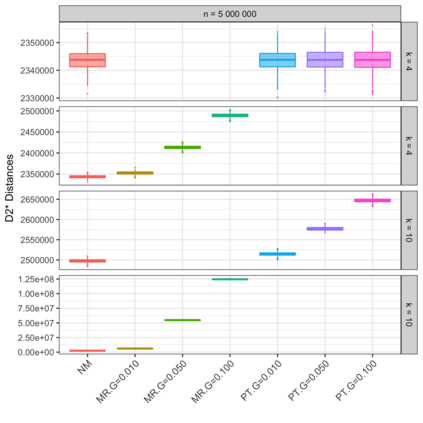
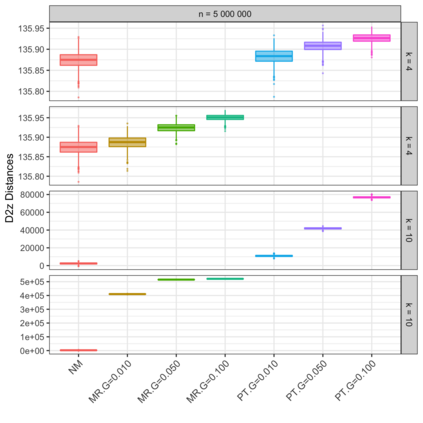
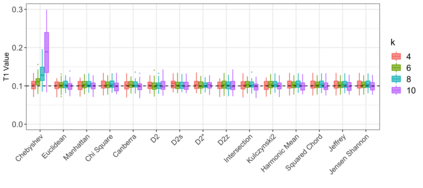
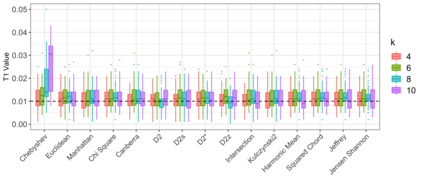
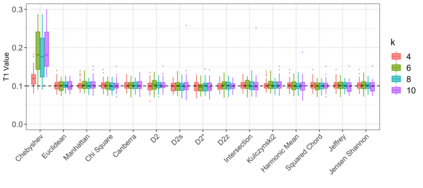
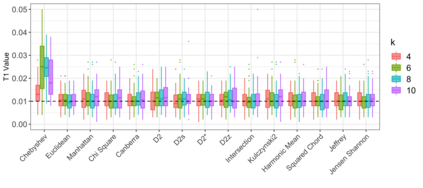
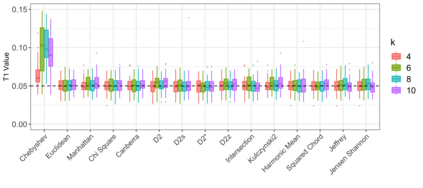
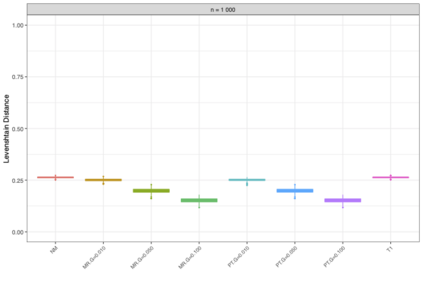
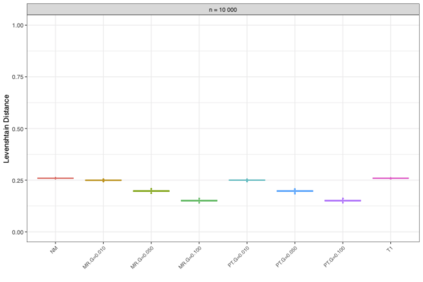
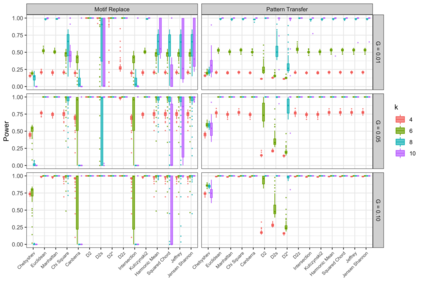
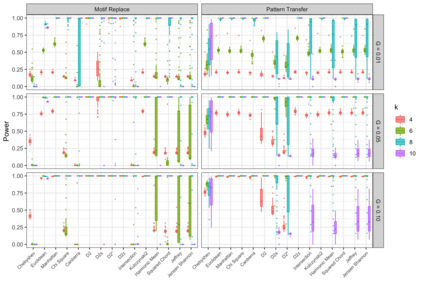
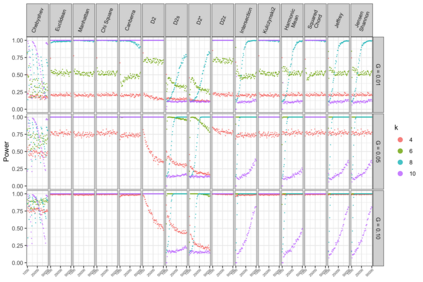
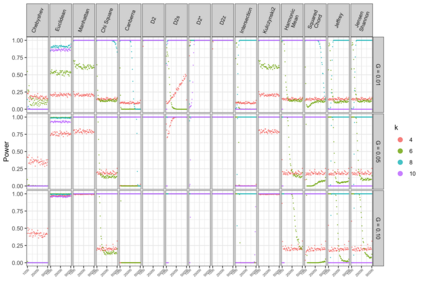
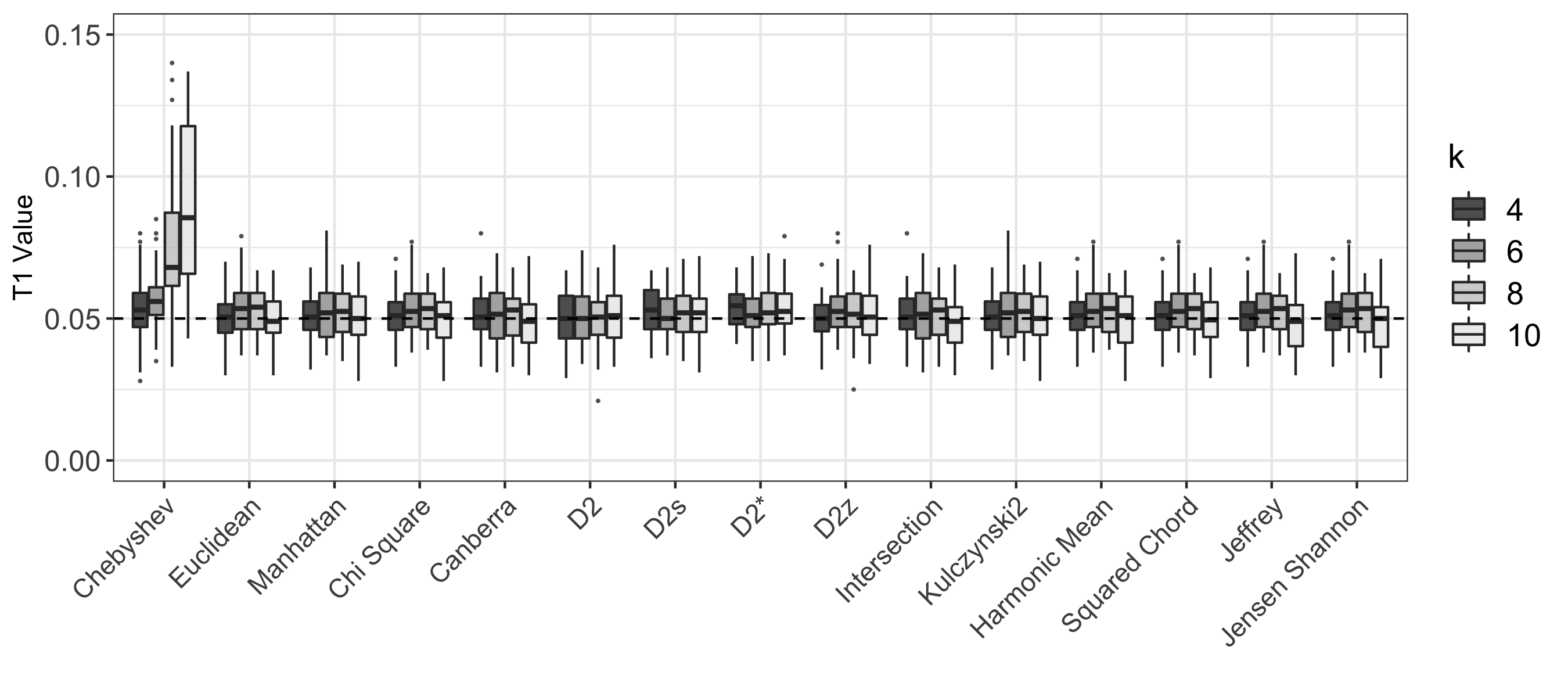
Motivation: Alignment-free (AF) distance/similarity functions are a key tool for sequence analysis. Experimental studies on real datasets abound and, to some extent, there are also studies regarding their control of false positive rate (Type I error). However, assessment of their power, i.e., their ability to identify true similarity, has been limited to some members of the D2 family by experimental studies on short sequences, not adequate for current applications, where sequence lengths may vary considerably. Such a State of the Art is methodologically problematic, since information regarding a key feature such as power is either missing or limited. Results: By concentrating on a representative set of word-frequency based AF functions, we perform the first coherent and uniform evaluation of the power, involving also Type I error for completeness. Two Alternative models of important genomic features (CIS Regulatory Modules and Horizontal Gene Transfer), a wide range of sequence lengths from a few thousand to millions, and different values of k have been used. As a result, we provide a characterization of those AF functions that is novel and informative. Indeed, we identify weak and strong points of each function considered, which may be used as a guide to choose one for analysis tasks. Remarkably, of the fifteen functions that we have considered, only four stand out, with small differences between small and short sequence length scenarios. Finally, in order to encourage the use of our methodology for validation of future AF functions, the Big Data platform supporting it is public.