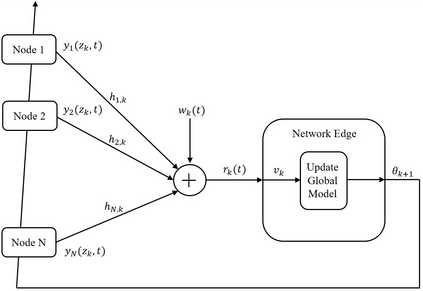
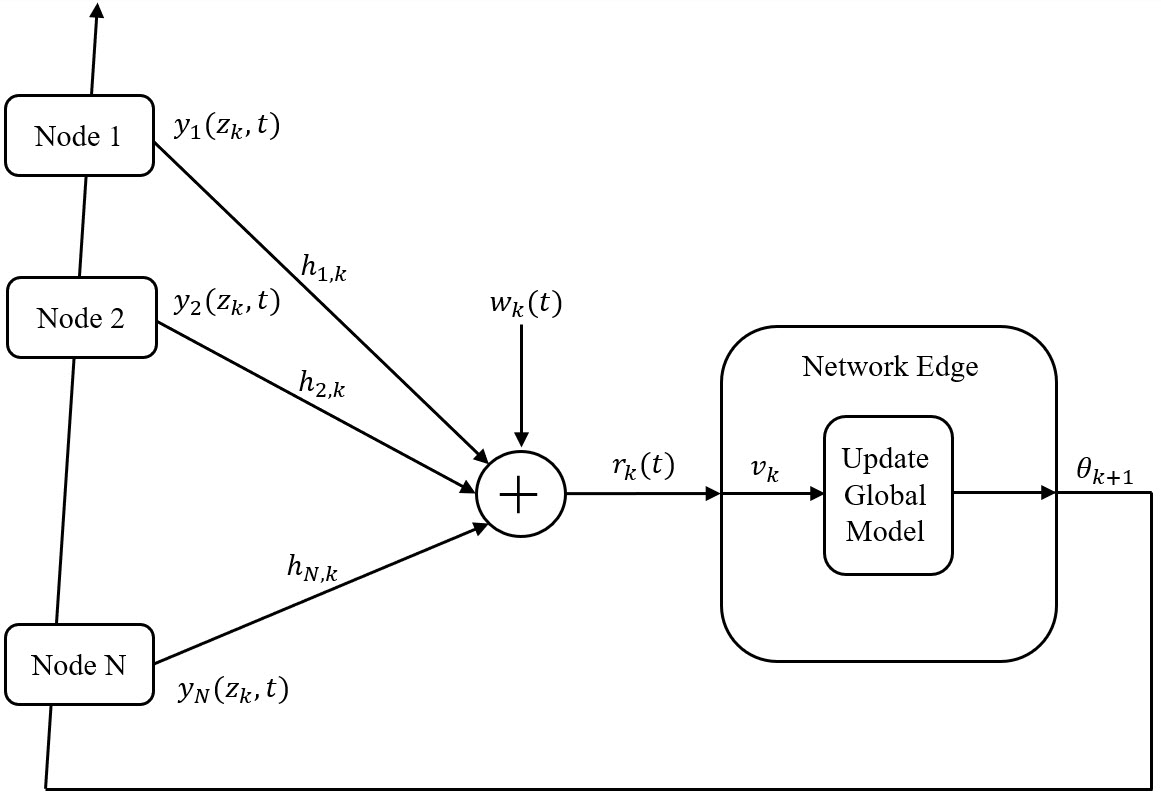
We consider a distributed learning problem in a wireless network, consisting of N distributed edge devices and a parameter server (PS). The objective function is a sum of the edge devices' local loss functions, who aim to train a shared model by communicating with the PS over multiple access channels (MAC). This problem has attracted a growing interest in distributed sensing systems, and more recently in federated learning, known as over-the-air computation. In this paper, we develop a novel Accelerated Gradient-descent Multiple Access (AGMA) algorithm that uses momentum-based gradient signals over noisy fading MAC to improve the convergence rate as compared to existing methods. Furthermore, AGMA does not require power control or beamforming to cancel the fading effect, which simplifies the implementation complexity. We analyze AGMA theoretically, and establish a finite-sample bound of the error for both convex and strongly convex loss functions with Lipschitz gradient. For the strongly convex case, we show that AGMA approaches the best-known linear convergence rate as the network increases. For the convex case, we show that AGMA significantly improves the sub-linear convergence rate as compared to existing methods. Finally, we present simulation results using real datasets that demonstrate better performance by AGMA.
翻译:我们认为,无线网络中存在着分布式学习问题,包括N分布式边缘装置和一个参数服务器(PS)。客观功能是边缘装置当地损失功能的总和,目的是通过多个接入频道(MAC)与PS沟通来训练一个共同模式。这个问题吸引了对分布式遥感系统的兴趣,以及最近对联结学习的兴趣,即所谓的超天计算。在本文中,我们开发了一个新型的加速渐渐白多重访问算法(AGMA)算法,该算法使用以动力为基础的梯度信号超过超音速淡化的MAC来提高与现有方法相比的趋同率。此外,AGMA并不要求权力控制或成型来取消淡化效应,这种效应会简化执行的复杂性。我们从理论上分析AGMA,并将错误的有限缩略图与Lipschitz梯度联系起来。在强烈的 convex案中,我们显示AGMA随着网络的增加而接近最著名的线性趋同率。在 convex案中,我们展示了AGMA目前采用真实的模版数据模拟方法,以更好地展示目前的数据趋同率。