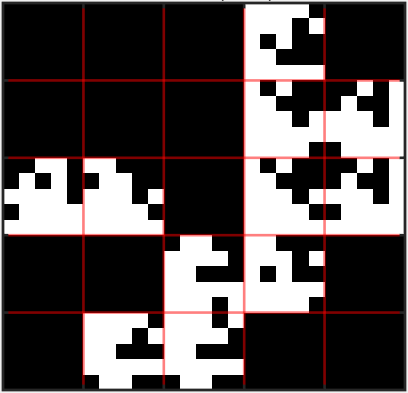
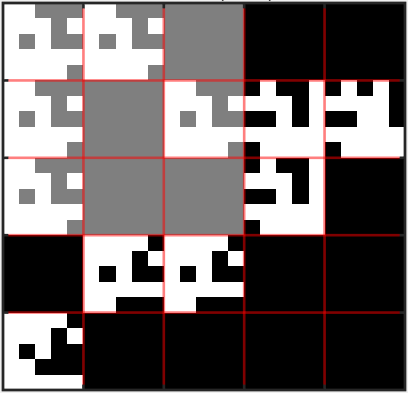
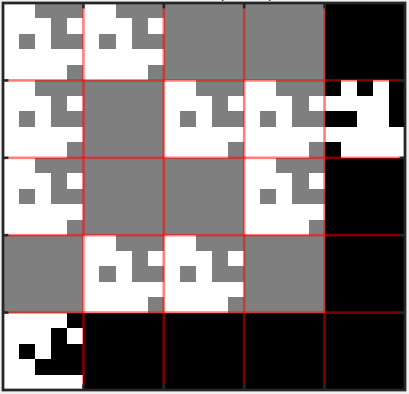
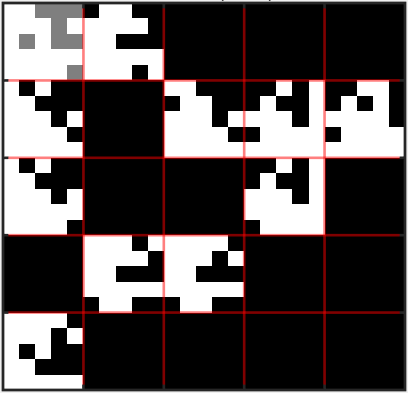
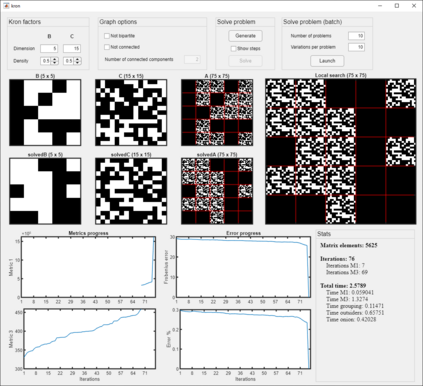
In this paper we describe a heuristic for decomposing a directed graph into factors according to the direct product (also known as Kronecker, cardinal or tensor product). Given a directed, unweighted graph~$G$ with adjacency matrix Adj($G$), our heuristic searches for a pair of graphs~$G_1$ and~$G_2$ such that $G = G_1 \otimes G_2$, where $G_1 \otimes G_2$ is the direct product of~$G_1$ and~$G_2$. For undirected, connected graphs it has been shown that graph decomposition is "at least as difficult" as graph isomorphism; therefore, polynomial-time algorithms for decomposing a general directed graph into factors are unlikely to exist. Although graph factorization is a problem that has been extensively investigated, the heuristic proposed in this paper represents -- to the best of our knowledge -- the first computational approach for general directed, unweighted graphs. We have implemented our algorithm using the MATLAB environment; we report on a set of experiments that show that the proposed heuristic solves reasonably-sized instances in a few seconds on general-purpose hardware.
翻译:在本文中,我们描述了一种将定向图表按照直接产品(又称Kronecker、红衣或加仑产品)分解成各种因素的超常现象。鉴于一个直接的、未加权的图形~G$和相邻矩阵Adj($G$)($G$),我们不太可能对一对图形进行超时搜索,以将一般定向图表分解成各种因素。尽管对图形因数化是一个已广泛调查的问题,但本文中提议的图因数化是我们所了解的最好的 -- -- 用于一般定向、非加权图表的首次计算方法;对于非定向、连接的图表,我们已显示,图形分解的“至少”与图形无异形学一样“困难”;因此,不可能存在将一般定向图表分解成各种因素的多元-时间算法。尽管图表因数化是一个问题,但据我们所知,本文中提议的图因数美元代表了 -- -- 用于一般定向、非加权图表的首次计算方法。关于非定向图表的图解剖图的首次计算方法。我们已用一个合理的硬化模型在一般环境上应用了一套硬化的硬体模型,我们在数秒内,我们已用了一套硬化了一套硬化的硬分析了。我们提出的硬分析。