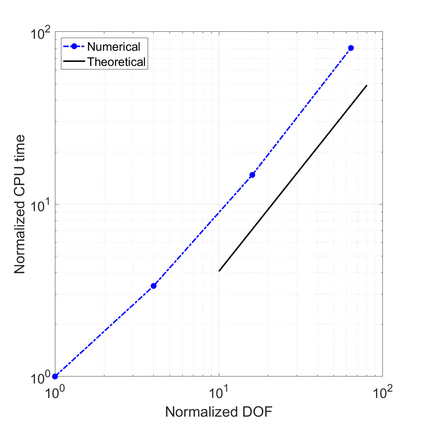
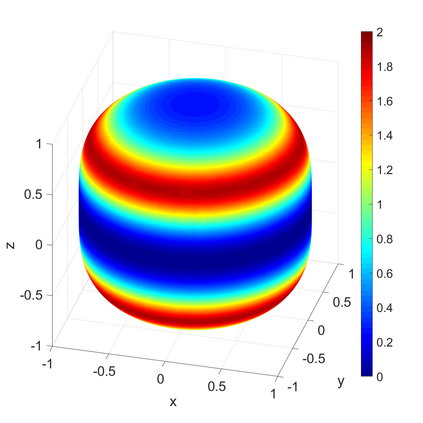
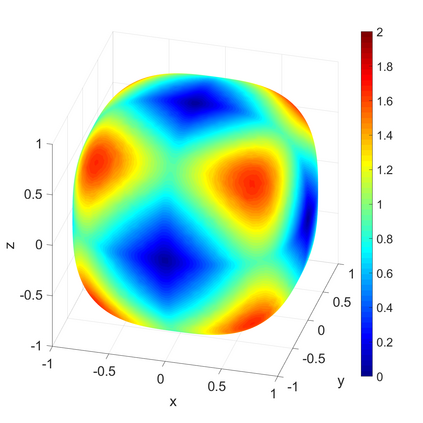
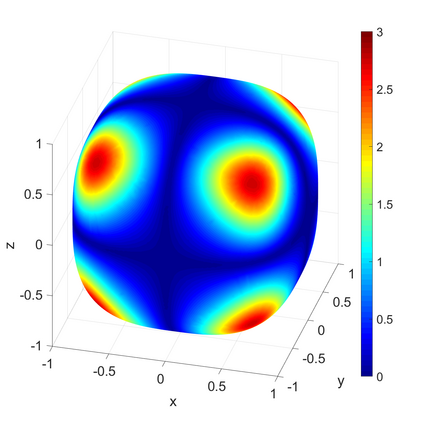
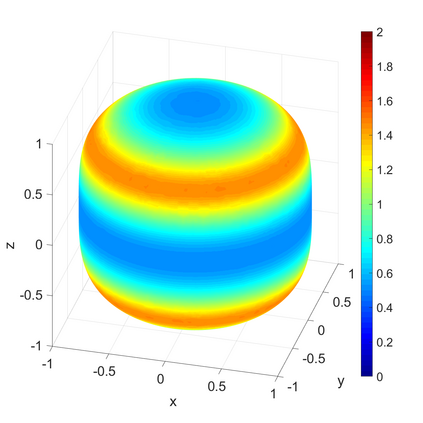
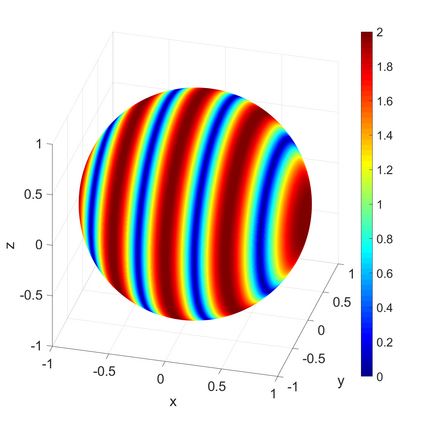
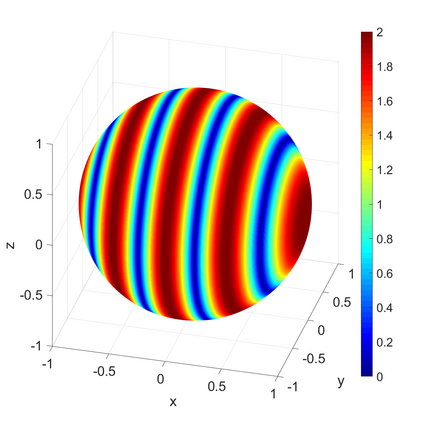
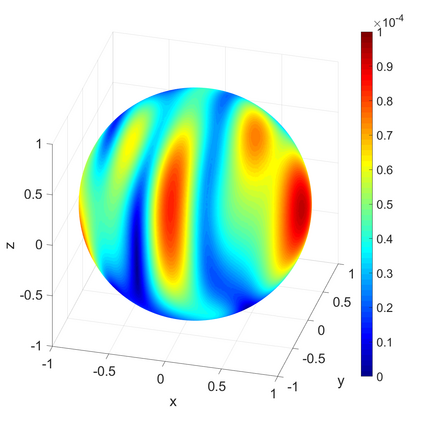
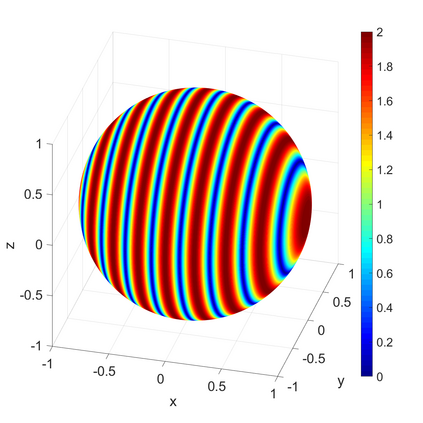
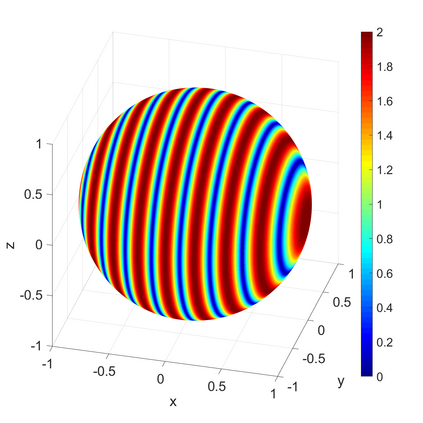
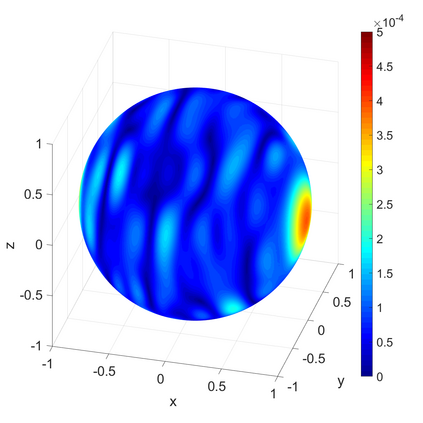
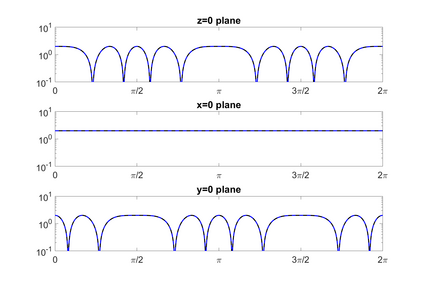
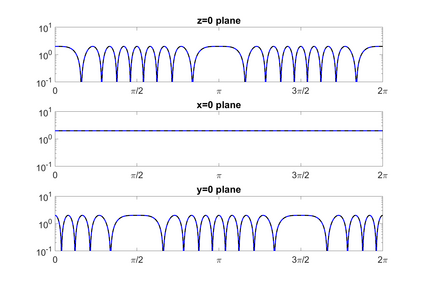
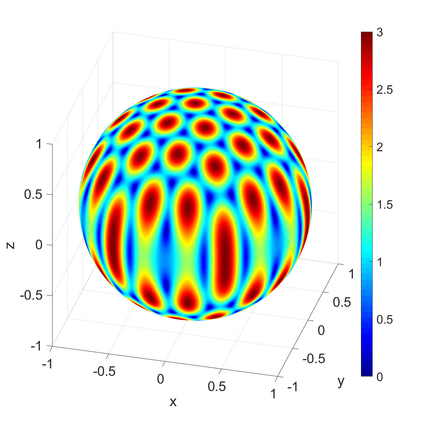
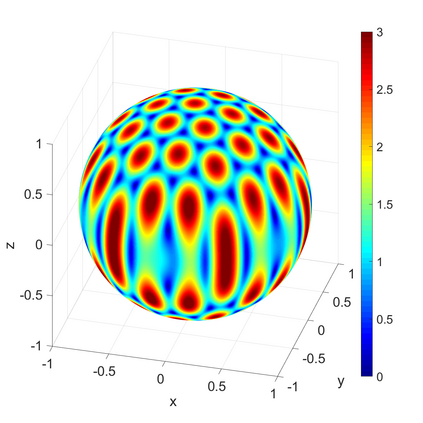
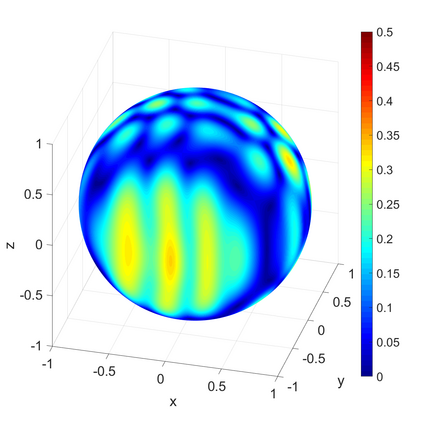
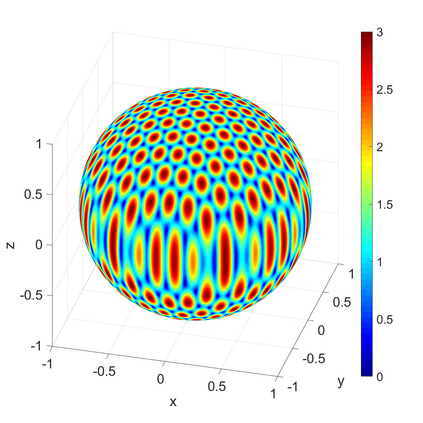
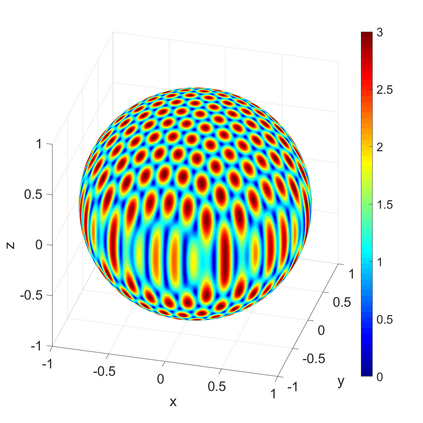
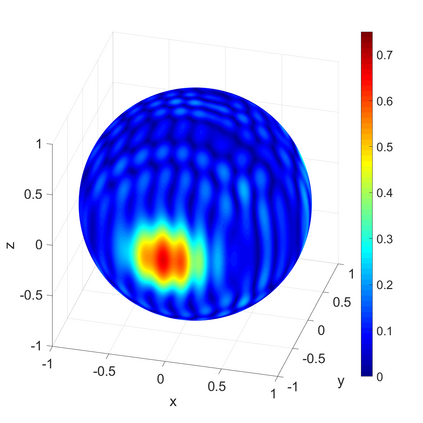
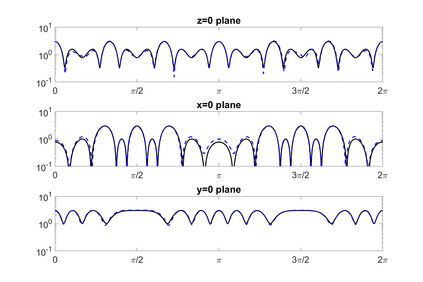
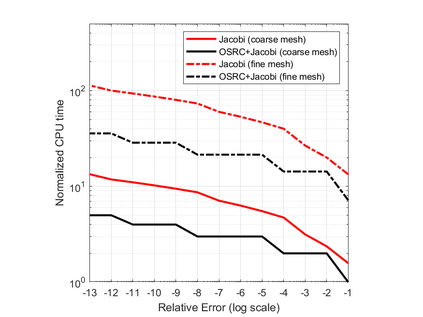
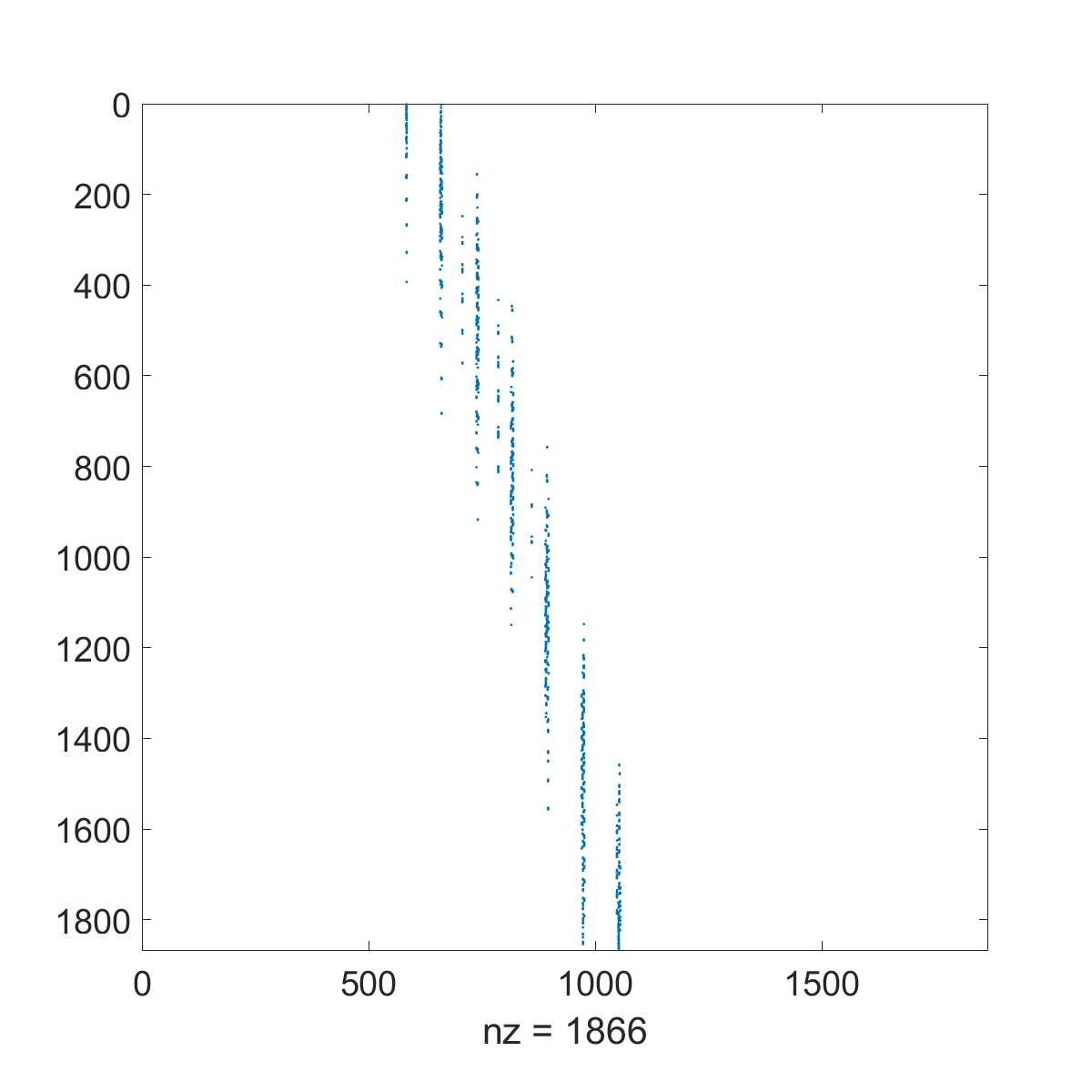
We propose a novel on-surface radiation condition to approximate the outgoing solution to the Helmholtz equation in the exterior of several impenetrable convex obstacles. Based on a local approximation of the Dirichlet-to-Neumann operator and a local formula for wave propagation, this new method simultaneously accounts for the outgoing behavior of the solution as well as the reflections arising from the multiple obstacles. The method involves tangential derivatives only, avoiding the use of integration over the surfaces of the obstacles. As a consequence, the method leads to sparse matrices and O(N) complexity. Numerical results are presented to illustrate the performance of the proposed method. Possible improvements and extensions are also discussed.
翻译:我们提出一个新的地表辐射条件,以近似Helmholtz等方程式在几个难以渗透的孔隙障碍的外部的离线解决方案。根据Drichlet-Neumann操作员的当地近似值和波传播的当地公式,这一新方法同时说明了解决方案的离线行为以及多重障碍产生的反射。这种方法仅涉及相近衍生物,避免了在障碍表面的融合。因此,该方法导致矩阵稀少和O(N)复杂性。提出了数字结果,以说明拟议方法的性能。还讨论了可能的改进和扩展。
相关内容
- Today (iOS and OS X): widgets for the Today view of Notification Center
- Share (iOS and OS X): post content to web services or share content with others
- Actions (iOS and OS X): app extensions to view or manipulate inside another app
- Photo Editing (iOS): edit a photo or video in Apple's Photos app with extensions from a third-party apps
- Finder Sync (OS X): remote file storage in the Finder with support for Finder content annotation
- Storage Provider (iOS): an interface between files inside an app and other apps on a user's device
- Custom Keyboard (iOS): system-wide alternative keyboards
Source: iOS 8 Extensions: Apple’s Plan for a Powerful App Ecosystem