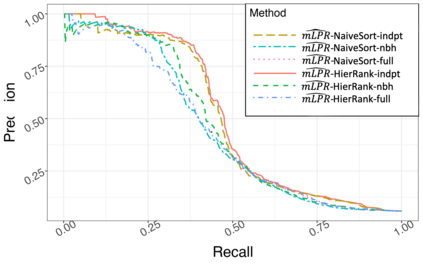
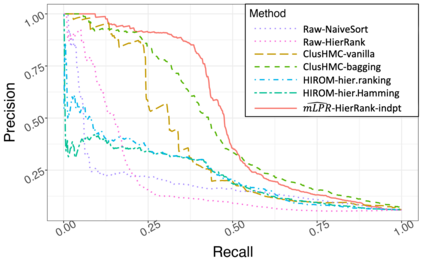
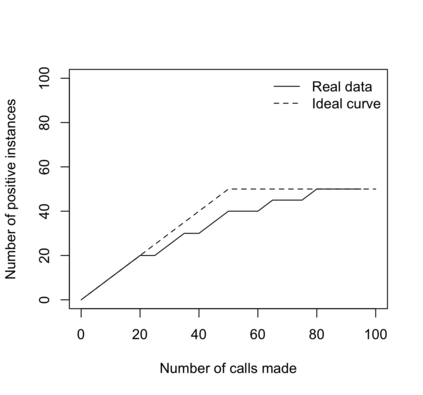
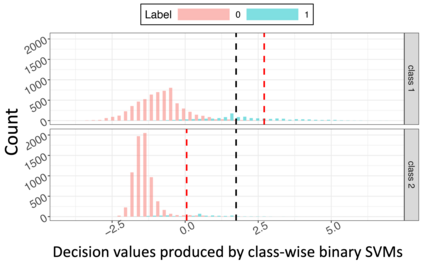
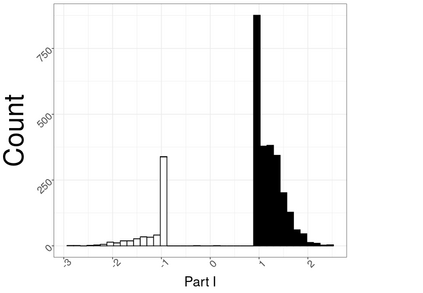
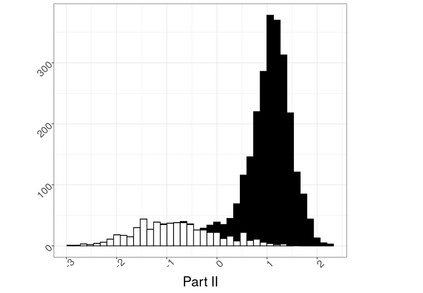
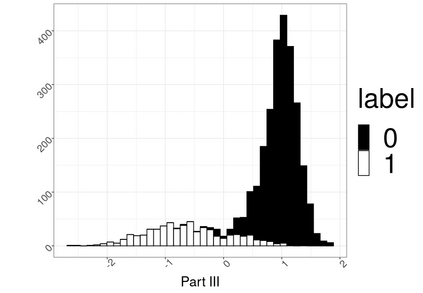
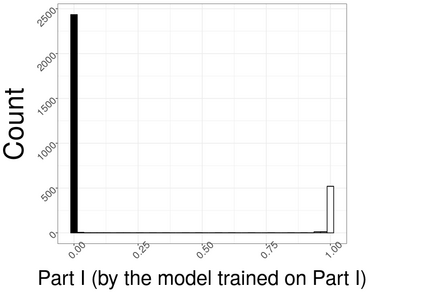
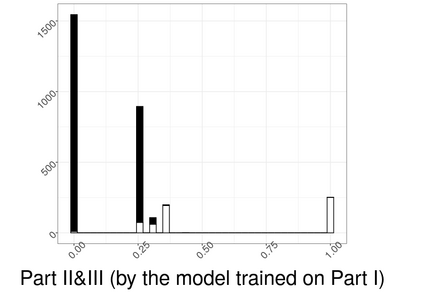
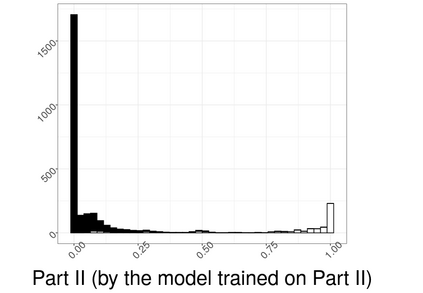
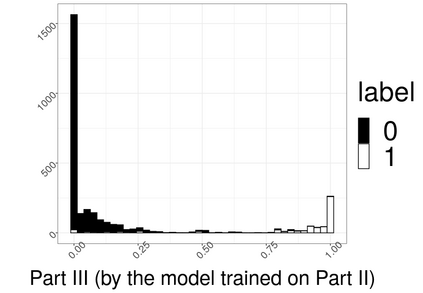
Hierarchical multi-label classification (HMC) has drawn increasing attention in the past few decades. It is applicable when hierarchical relationships among classes are available and need to be incorporated along with the multi-label classification whereby each object is assigned to one or more classes. There are two key challenges in HMC: i) optimizing the classification accuracy, and meanwhile ii) ensuring the given class hierarchy. To address these challenges, in this article, we introduce a new statistic called the multidimensional local precision rate (mLPR) for each object in each class. We show that classification decisions made by simply sorting objects across classes in descending order of their true mLPRs can, in theory, ensure the class hierarchy and lead to the maximization of CATCH, an objective function we introduce that is related to the area under a hit curve. This approach is the first of its kind that handles both challenges in one objective function without additional constraints, thanks to the desirable statistical properties of CATCH and mLPR. In practice, however, true mLPRs are not available. In response, we introduce HierRank, a new algorithm that maximizes an empirical version of CATCH using estimated mLPRs while respecting the hierarchy. The performance of this approach was evaluated on a synthetic data set and two real data sets; ours was found to be superior to several comparison methods on evaluation criteria based on metrics such as precision, recall, and $F_1$ score.
翻译:在过去几十年里,多等级的多标签分类(HMC)引起了越来越多的注意。当各等级之间的等级关系存在时,这种分类就适用,并且需要与多标签的分类一起纳入,因为每个对象被分配到一个或一个以上的类别。 HMC有两个关键的挑战:i)优化分类的准确性,同时确保给定的等级。为了应对这些挑战,我们在本篇文章中引入了一个新的统计数据,称为每个类别每个对象的多维地方精确率(MLPR)。但是,我们表明,通过简单地按其真实的 mLPR的降序对不同类别对象进行分类,作出的分类决定在理论上可以确保等级的等级并导致最大程度的CATCH,这是我们引入的目标功能之一,即:一是优化分类的准确性,同时确保分类的分类准确性。由于CATCH和 mLPR1 的统计特性,在实践中,没有真正的 mLPR1 。作为回应,我们引入了HierRank, 一种新的算法,即最大限度地实现CATCH的高级等级性评估,同时用估计的模型评估了我们的标准。