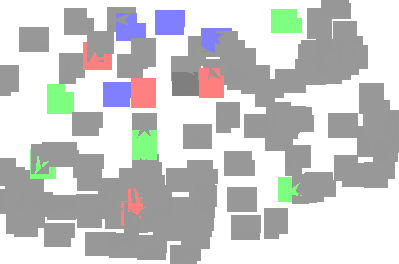
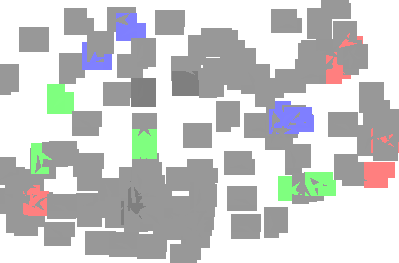
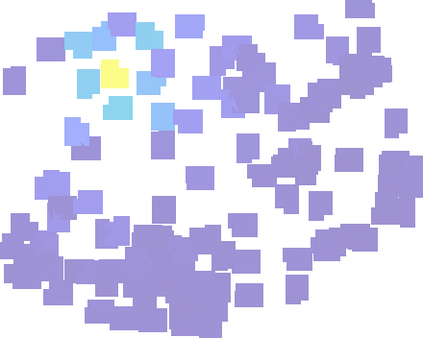
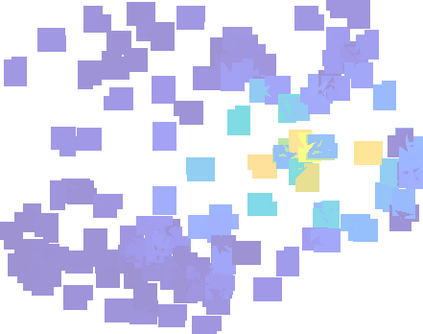
We study linear filters for processing signals supported on abstract topological spaces modeled as simplicial complexes, which may be interpreted as generalizations of graphs that account for nodes, edges, triangular faces etc. To process such signals, we develop simplicial convolutional filters defined as matrix polynomials of the lower and upper Hodge Laplacians. First, we study the properties of these filters and show that they are linear and shift-invariant, as well as permutation and orientation equivariant. These filters can also be implemented in a distributed fashion with a low computational complexity, as they involve only (multiple rounds of) simplicial shifting between upper and lower adjacent simplices. Second, focusing on edge-flows, we study the frequency responses of these filters and examine how we can use the Hodge-decomposition to delineate gradient, curl and harmonic frequencies. We discuss how these frequencies correspond to the lower- and the upper-adjacent couplings and the kernel of the Hodge Laplacian, respectively, and can be tuned independently by our filter designs. Third, we study different procedures for designing simplicial convolutional filters and discuss their relative advantages. Finally, we corroborate our simplicial filters in several applications: to extract different frequency components of a simplicial signal, to denoise edge flows, and to analyze financial markets and traffic networks.
翻译:我们的研究线性过滤器,用于处理以简易复合物为模型的抽象表层空间所支持的信号,这些过滤器可以被解释为计算复杂度低的分布式图解,因为它们只涉及(多轮)在相邻的上下两端孔径形形形形形形形形形形形色色色色色色等。为了处理这些信号,我们开发了简化的共生过滤器,其定义是下层和上层Hodge Laplicas的矩阵多波形形色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色的特征。这些色色色色色色色色色色色色色色色色色色色和上层色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色调,这些色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色色的图图图图图图图图的图的图的图, 和色的图图的图图,这些, 和色色色色色调的图图图图图图图图图,,,, 的图图图图图图图图图图图图图图图,, 的图图, 、图图图图图图图, 、图图图图图图图图图图图图图图图图,,,,,,,,,,,,,,,,,,,,,我们,,,我们,,,,,,,,,我们