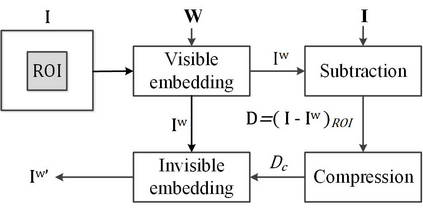
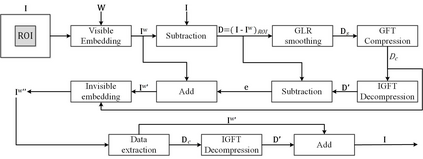
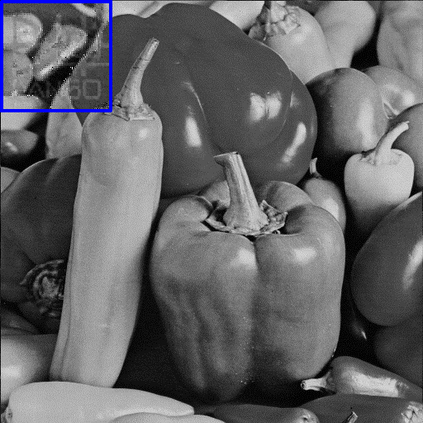
Reversible visible watermarking (RVW) is an active copyright protection mechanism. It not only transparently superimposes copyright patterns on specific positions of digital images or video frames to declare the copyright ownership information, but also completely erases the visible watermark image and thus enables restoring the original host image without any distortion. However, existing RVW algorithms mostly construct the reversible mapping mechanism for a specific visible watermarking scheme, which is not versatile. Hence, we propose a generic RVW framework to accommodate various visible watermarking schemes. In particular, we obtain a reconstruction data packet -- the compressed difference image between the watermarked image and the original host image, which is embedded into the watermarked image via any conventional reversible data hiding method to facilitate the blind recovery of the host image. The key is to achieve compact compression of the difference image for efficient embedding of the reconstruction data packet. To this end, we propose regularized Graph Fourier Transform (GFT) coding, where the difference image is smoothed via the graph Laplacian regularizer for more efficient compression and then encoded by multi-resolution GFTs in an approximately optimal manner. Experimental results show that the proposed framework has much better versatility than state-of-the-art methods. Due to the small amount of auxiliary information to be embedded, the visual quality of the watermarked image is also higher.
翻译:翻版可见水标记( RVW) 是一个积极的版权保护机制。 它不仅透明地在数字图像或视频框架的具体位置上添加版权模式, 以宣布版权所有权信息, 而且完全删除可见的水标记图像, 从而能够恢复原主机图像, 而不出现任何扭曲。 然而, 现有的 RVW 算法大多为特定可见水标记方案构建可翻版绘图机制, 且不具有多功能性。 因此, 我们提出一个通用的 RVW 框架, 以适应各种可见水标记方案。 特别是, 我们获得一个重建数据包 -- -- 水标记图像和原始主机主机图像之间的压缩差异图像, 通过任何传统的可变现数据隐藏方法嵌入水标记图像, 以便于盲目的恢复主机图像。 关键是要对差异图像进行压缩, 以高效地嵌入重建数据包。 为此, 我们提议固定化图 Fourier 变换( GFEFRT) 编码, 其差异图像通过图表平滑动, 以便更高效地压缩, 然后通过多分辨率图像编码化为原始主机质量框架, 也以最优化的方式显示小的GFFIFTFIFIFIFIFIFIFT 。 。