Are energy savings the only reason for the emergence of bird echelon formation?

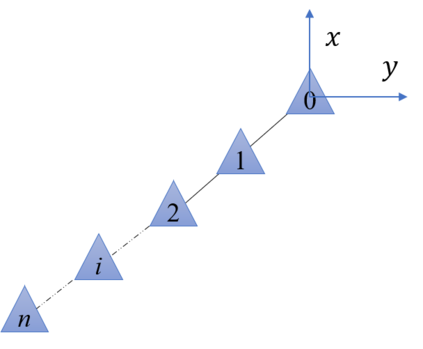
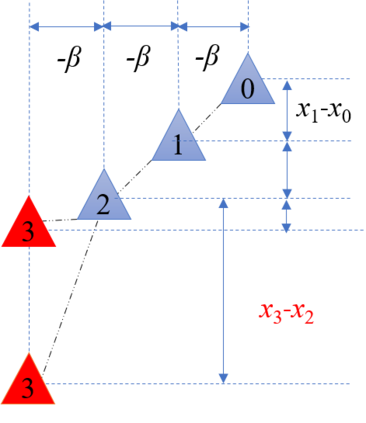
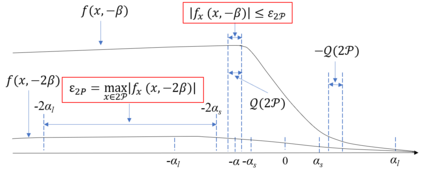
We analyze the conditions under which the emergence of frequently observed echelon formation can be explained solely by the maximization of energy savings. We consider a two-dimensional multi-agent echelon formation, where each agent receives a benefit that depends on its position relative to the others, and adjusts its position to increase this benefit. We analyze the selfish case where each agent maximizes its own benefit, leading to a Nash-equilibrium problem, and the collaborative case in which agents maximize the global benefit of the group. We provide conditions on the benefit function under which the frequently observed echelon formations cannot be Nash equilbriums or group optimums. We then show that these conditions are satisfied by the conventionally used fixed-wing wake benefit model. This implies that energy saving alone is not sufficient to explain the emergence of the migratory formations observed, based on the fixed-wing model. Hence, either non-aerodynamic aspects or a more accurate model of bird dynamics should be considered to construct such formations.